Сравнение первой степени

Определение Выражение ax ≡ b mod m называется сравнением первой степени с одним неизвестным. Решить сравнение – значит найти все значения x, которые довлетворяют данному сравнению.

Теорема. Если (a, m) = d, т. е. число a и модуль m имеет общий делитель d, причем число d не делит b, то сравнение ax ≡ b mod m не имеет решений.

Теорема. Если (a, m) = 1, т. е. числа a и m взаимнопросты, то сравнение ax ≡ b mod m имеет одно и только одно решение.

Теорема. Если (a, m) = 1, т.е числа a и b взаимно простые, то решением сравнения ax ≡ b mod m является класс x ≡ baϕ (m)-1 mod m, где φ(m) – значение функции Эйлера для модуля m.

Признак делимости, обращение об. дроби в систематическую

Рассмотрим некоторые вопросы элементарной арифметики, изучение которых упрощается применением теории сравнений.

Пример 1. Вывести признак делимости на 11 в десятичной системе счисления.

Решение. Разобьем цифровую запись числа на группы по две цифры в каждой группе (разбиение ведется справа налево). Получим

, так как .

Отсюда вытекает признак делимости на 11.

1. Нахождение остатков при делении числа на данное число (этот вопрос мы рассматривали в теме теоремы Эйлера и Ферма)

Теорема 1. Любую положительную правильную дробь вида можно представить в виде конечной суммы ,где при всех имеем 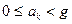. Вместо записи (1) обычно пишут так: Теорема 2. Правильная несократимая дробь может быть представлена в виде:

в том и том случае, когда в разложение знаменателя на простые множители входят только те простые числа, которые участвуют и в разложении на простые множители основания .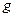

Дата добавления: 2015-07-20