Свойства сравнений.

1°. Отношение сравнимости является отношением эквивалентности, то есть является отношением рефлексивным, симметричным, транзитивным:

1) 2) ,

3) .

2°. Сравнения можно почленно складывать, вычитать и перемножать:

если то .

Доказательство. .

3°. Обе части сравнения можно разделить на их общий делитель 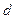, если он взаимно прост с модулем :

.

4°. Обе части сравнения и модуль можно разделить на их общий делитель :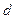

.

5°. Если сравнение 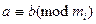имеет место по нескольким модулям, где 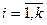, то оно имеет место и по модулю, являющемуся наименьшим общим кратным этих модулей, в частности,

Следствия. Обе части сравнения можно умножать на любое целое число.

К обеим частям сравнения можно прибавить любое целое число. К любой части сравнения можно прибавить произвольное число, кратное модулю. Сравнения можно возводить в любую натуральную степень. Обе части сравнения и модуль можно умножать на одно и тоже натуральное число.

Теорема 2. Пусть .

Если , то .

В частности, , отсюда получаем признак делимости на 9. Аналогично из теоремы можно получить и другие признаки делимости.

2. Кольцо классов вычетов по заданному модулю.

Определение 2. Класс вычетов по модулю называется множество чисел .

Пример. Пусть 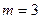, тогда кольцо целых чисел разобьется на три класса вычетов:

, числа, при делении которых на 3 получается остаток 0,

, числа, при делении которых на 3 получается остаток 1,

, числа, при делении которых на 3 получается остаток 2.

Определение 3. Суммой (произведением) двух классов вычетов и 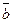по заданному модулю будем называть класс, которому принадлежит число (): , .

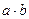Теорема 3. Пусть 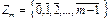, тогда множество классов вычетов по заданному модулю относительно сложения и умножения является коммутативным кольцом с единицей, причем по составному модулю оно имеет делители нуля, а по простому модулю является полем (пример конечного поля).

Следствие. Множество классов вычетов по простому модулю без нуля относительно умножения является группой.

П.3. Системы вычетов.

В каждом классе вычетов по модулю можно найти наименьший неотрицательный вычет – остаток от деления 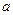на : 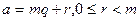, и абсолютно наименьший вычет – вычет, абсолютная величина, которого меньше абсолютных величин всех других вычетов этого же класса.

Определение 4. Совокупность чисел, взятых по одному из каждого класса вычетов по заданному модулю , называется полной системой вычетов по модулю (ПСВ). ПСВ содержит чисел и они между собой не сравнимые по модулю .

Приведенной системой вычетов по модулю (ПрСВ) называется часть ПСВ, которая состоит из чисел, взаимно простых с . ПрСВ состоит из (функция Эйлера) чисел, которые взаимно просты с и не сравнимы по модулю .

Теорема 4. Если и пробегает ПСВ по модулю , то также пробегает ПСВ по модулю . Если же и пробегает ПрСВ по модулю , то также пробегает ПрСВ по модулю .

Дата добавления: 2015-07-20