Читайте также:
|
Определение 1. Пусть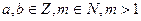 
. Целые числа 
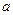и 
называют сравнимыми по модулю 
, если 
. Обозначение: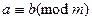 
.
Примеры.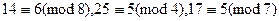 
.
Теорема 1. 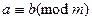тогда и только тогда, когда 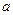и при делении на имеют равные остатки, то есть являются равноостаточными.
Доказательство. По теореме о делении с остатком получаем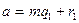 
, 
, 
. Тогда 
, по свойствам делимости из последнего соотношения вытекает утверждение теоремы.
Дата добавления: 2015-07-20; просмотров: 44 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| При расчете общих индексов выбор формулы зависит от характера информации об индексируемой величине и соизмерителе (весе) индексов. | | | Свойства сравнений. |