
Читайте также:
|
Последовательность 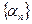 называется бесконечно малой (б.м.), если
называется бесконечно малой (б.м.), если  αn =0, т.е. если
αn =0, т.е. если 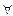 ε >0
ε >0  n 0
n 0  n>n 0 | αn |< ε.
n>n 0 | αn |< ε.
Последовательность { An } называется бесконечно большой (б.б.), если  An, т.е. если
An, т.е. если  А> 0
А> 0  n 0
n 0  n>n 0 | An | >A.
n>n 0 | An | >A.
Фактически мы дали сейчас определение бесконечного предела последовательности. Аналогично можно дать определение бесконечного предела определенного знака:

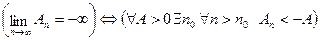 .
.
Пример 14.8. Как показывает пример 14.3, последовательность xn = 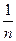 , n Î N, – б. м., т.к.
, n Î N, – б. м., т.к. 
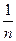 = 0.
= 0.
Последовательность βп = n, n Î N, – б.б., это вытекает непосредственно из принципа Архимеда:  βn =+¥.
βn =+¥.
Свойства б.м. б.б. последовательностей:
1. Сумма двух б.м. последовательностей является б.м. последовательностью, т.е. если { αn }- б.м., { βn }- б.м., то их сумма { αn + βn } – б.м. последовательность.
Доказательство. α n – б.м., т.е.  ε >0
ε >0  n 1
n 1  n > n 1 | αn |<
n > n 1 | αn |< 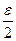 ; βn – б.м., т.е.
; βn – б.м., т.е.  ε >0
ε >0  n 2
n 2  n > n 2 | βn |<
n > n 2 | βn |< 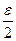 . Положим n 0=max { n 1, n 2}, тогда для всех n > n 0 выполняется оба неравенства одновременно, поэтому
. Положим n 0=max { n 1, n 2}, тогда для всех n > n 0 выполняется оба неравенства одновременно, поэтому
| αn + βn |≤| αn |+| βn |< 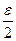 +
+ 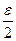 = ε.
= ε.
Итак,  ε >0
ε >0  n 0
n 0  n > n 0 | αn + βn |< ε, т.е.
n > n 0 | αn + βn |< ε, т.е.  (αn + βn)=0, а последовательность { αn + βn } является б.м.
(αn + βn)=0, а последовательность { αn + βn } является б.м.
Из этого свойства ясно, что сумма конечного числа б.м. последовательностей является б.м. последовательностью.
2. Произведение б.м. последовательности на ограниченную последовательность является б.м., т.е. если { αn } – б.м., { xn } – ограниченная последовательности, то { αn • xn }– б.м. последовательность.
Доказательство. Последовательность { xn } ограничена, это означает, что существует число М> 0 такое, что | xn |≤ M  n Î N. Выберем произвольное число ε >0 и положим ε 1=
n Î N. Выберем произвольное число ε >0 и положим ε 1= 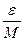 . Так как αn – б.м. последовательность, то для ε 1
. Так как αn – б.м. последовательность, то для ε 1  n 0
n 0  n > n 0 | αn |< ε 1. Тогда
n > n 0 | αn |< ε 1. Тогда
| αn • xn |=| αn |•| xn |< ε 1• M= 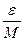 • M = ε.
• M = ε.
Таким образом,  ε >0
ε >0  n 0
n 0  n > n 0 | αnxn |< ε. т.е. последовательность { αnxn }– б.м.
n > n 0 | αnxn |< ε. т.е. последовательность { αnxn }– б.м.
Следствия. 1) Если{ αn }– б.м. последовательность, с =const (постоянная), то { cαn } – б.м. последовательность (произведение б.м. последовательности на константу является б.м. последовательностью).
2) { αn }, { βn }– б.м. последовательности, тогда { αnβn }– б.м. последовательность (произведение двух или конечного числа б.м. последовательностей является б.м. последовательностью).
3. Связь б.м. и б.б. последовательностей: обратная к б.м. последовательности является б.б. последовательность и наоборот, т.е.
{ αn }- б.м. и αn ≠0  n =>
n => 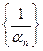 - б.б.,
- б.б.,
{ βn }- б.б. и βn ≠0  n =>
n => 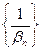 - б.м.
- б.м.
Доказательство. Пусть αn – б.м. и βn = 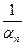 , и пусть М >0. Так как последовательность αn – б.м., то для числа ε=
, и пусть М >0. Так как последовательность αn – б.м., то для числа ε= 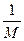 >0
>0  n 0
n 0  n > n 0 | αn |< ε =
n > n 0 | αn |< ε = 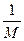 , или
, или
| βn | = 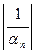 >
> 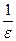 = M,
= M,
но это и означает, что βn = 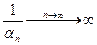 , т.е. является б.б.
, т.е. является б.б.
Теорема 14.2. Последовательность { xn } имеет своим пределом число а:  xn = а, тогда и только тогда, когда xn = а + αn, где { αn } – б.м. последовательность, т.е.
xn = а, тогда и только тогда, когда xn = а + αn, где { αn } – б.м. последовательность, т.е.

 xn = а ó (xn= a + αn, где αn – б.м.).
xn = а ó (xn= a + αn, где αn – б.м.).
Доказательство. Необходимость. Если  xn = a, то
xn = a, то  ε >0
ε >0  n 0
n 0  n > n 0 | xn - a | < ε. Положим αn = xn - a, тогда xn= a + αn и αn – б. м.. Действительно, последнее неравенство означает, что
n > n 0 | xn - a | < ε. Положим αn = xn - a, тогда xn= a + αn и αn – б. м.. Действительно, последнее неравенство означает, что  ε >0
ε >0  n 0
n 0  n > n 0
n > n 0 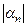 < ε, т.е. αn – б. м.
< ε, т.е. αn – б. м.
Обратно (достаточность). Пусть последовательность { xn } такова, что существует такое число a, что xn можно представить в виде xn= a + αn, где { αn } – б.м. Так как { αn } – б. м., то  ε >0
ε >0  n 0
n 0  n > n 0
n > n 0 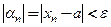 , но это и означает, что
, но это и означает, что  xn = a.
xn = a.
Дата добавления: 2015-07-20; просмотров: 173 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определение предела последовательности. | | | Арифметические свойства пределов последовательностей |