Арифметические свойства пределов последовательностей

Теорема 14.3. Если последовательность { x_n } сходится и x_n = а, то для любого числа с последовательность { cx_n } также сходится и

сx_n = са = с x_n,

т.е. постоянный множитель можно выносить за знак предела.

Доказательство. Так как число а является пределом последовательности x_n, то x_n = а + α_n, α_n – б.м. Но тогда сx_n = са + сα_n, где сα_n – б.м. (см. предыдущий пункт). Это означает (см. теорему 14.2), что число са есть предел последовательности { cx_n }.

Теорема 14.4. Если последовательности { x_n } и { y_n } сходятся и x_n = а, y_n = b, то последовательность { x_n + y_n } также сходится и

(x_n + y_n)= a+b = x_n + y_n,

т.е. предел суммы сходящихся последовательностей равен сумме пределов этих последовательностей.

Доказательство. Из условии теоремы вытекает, что x_n = а + α_n и y_n = b+ β_n, где α_n и β_n – б.м. последовательности, тогда

x_n + y_n =(a+b) + (α_n +β_n),

где α_n+β_n – б.м. Это и означает, см. теорему 14.2, что число a+b – предел последовательности { x_n + y_n }.

Теорема 14.5. Пусть последовательности { x_n } и { y_n } сходятся и x_n = а, y_n = b. Тогда последовательность { x_n y_n } также сходится и

x_n y_n = ab = x_n y_n,

т.е. предел произведения сходящихся последовательностей равен произведению их пределов.

Доказательство. По условию теоремы x_n = а + α_n и y_n = b+ β_n, где α_n и β_n – б.м. Тогда

x_nу=ab+ (b•α_n + a•β_n + α_n • β_n),

где b•α_n + a•β_n + α_n • β_n – б.м. (см. свойства б.м.), из теоремы 14.2 число ab и есть предел последовательности { x_n y_n }.

Из этой теоремы вытекает, что, если x_n = а, то

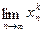= а^к =( x_n) ^к.

Теорема 14.6. Пусть последовательности { x_n } и { y_n } сходятся, x_n = а, y = b и b ≠0. тогда последовательность сходится и

= = ,

т.е. предел отношения сходящихся последовательностей равен отношению их пределов.

Принимаем эту теорему без доказательства.

Пример 14.9. Вычислить предел .

Решение. При n →¥ числитель и знаменатель стремятся к бесконечности (являются бесконечно большим). Действительно, 3 n ²-2 n +1= n ²(3- + ) , т.к. и – б.м., а 3- + ограничена как сходящаяся. Аналогично, знаменатель тоже стремится к бесконечности. Поэтому сразу применить теорему о пределе отношения нельзя (мы имеем т.н. неопределенность вида ), сначала вынесем в числителе и в знаменателе старшую степень n ², после чего применим теорему о пределе частного:

= = = =

= = = – .

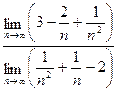Пример 14.10. Вычислим предел .

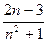Решение. 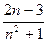= = = = 0,

т.к. при n ®¥ числитель 2- является ограниченной последовательностью (она имеет предел равный 2), а знаменатель 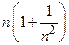– б.б., а обратная к ней .– б.м., а произведение ограниченной последовательности на б.м. является б.м.

14.7. Предельный переход в неравенствах

Теорема 14.7. Пусть и a>0. Тогда все члены последовательности >0, начиная с некоторого номера, т.е. n₀ n>n₀ >0.

Доказательство. По определению предела последовательности для e = >0 n₀ n>n₀ < e, т.е. a-e < x_n < a+e или x_n > a-e = >0. (см. рис. 14.5).

Теорема 14.8. Пусть последовательности { x_n } и { y_n } сходятся, , и x_n y_n, начиная с некоторого номера. Тогда a b, т.е. .

Теорема 14.9. (Теорема о трех последовательностях).

Пусть даны три последовательности { x_n },{ y_n },{ z_n }, причем { x_n } и { z_n } сходятся и 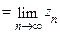. Если для всех nÎN x_n y_n z_n, то последовательность { y_n } тоже сходится и .

Доказательство. Для e >0 n₁ n>n₁ < e и n₂ n>n₂ < e или a -e < x_n < a+e и a -e < z_n < a+e.

Положим n₀ = max{ n₁,n₂ }. Тогда для всех n>n₀ выполняются оба неравенства одновременно. Тогда e >0 n₀ n>n₀

a - e < x_n y_n z_n < a+e,

т. е. 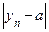< e, а это и означает, что последовательность { y_n } имеет своим пределом число a.

Из этой теоремы вытекает следующее полезное утверждение. Пусть даны две последовательности { x_n } и { y_n } и 0 x_n y_n для всех n. Тогда

если { x_n } – б. б., то { y_n } – б. б.,

если { y_n } – б. м., то { x_n } – б. м.

Дата добавления: 2015-07-20