Индуктивные множества. Натуральные числа. Метод математической индукции.

Множество Х Ì R называется индуктивным, если из условия x Î X вытекает, что x +1Î X.

Пересечение любого числа индуктивных множеств является индуктивным множеством.

Множеством натуральных чисел N Ì R называется наименьшее индуктивное множество, содержащее число 1:

1, 1+1, (1+1)+1, …,

или, в более привычных обозначениях: 1, 2, 3, ….

Метод математической индукции. Если некоторое высказывание, зависящее от номера n Î N, справедливо для n =1, и из справедливости этого высказывания для некоторого номера n вытекает его справедливость для номера n +1, то это высказывание справедливо для всех натуральных чисел n Î N.

Это непосредственно вытекает из определения множества натуральных чисел как наименьшего индуктивного множества, содержащего число 1.

Пример 13.2. Доказать методом математической индукции

1²+2²+…+ n ²= 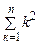= 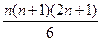(13.1)

Доказательство. При n =1 эта формула верна:

1²= =1.

Пусть эта формула верна для номера n Î N. Покажем, что тогда она верна для номера n +1. Действительно

1²+2²+…+ n ²+(n+ 1)²= 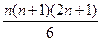+(n+ 1)²= 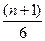[ n (2 n +1)+6(n +1)]= = 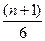[2 n ²+ n+ 6 n +6]= 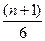[2 n ²+7 n +6]= .

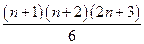Это же число получится, если в правую часть формулы (13.1) вместо n подставить n +1. Итак, формула (13.1) доказана.

Пример 13.3. Бином Ньютона. (a+b) ⁿ.

Выведем формулу бинома Ньютона. Введем некоторые обозначения:

n! = n •(n- 1)•…•2•1 –"эн- факториал" – произведение всех натуральных чисел от 1 до n.

Ясно, что 1!=1, 2!=2, 3!= 6, 4!= 24, 5!=120, (n +1)!=(n +1)• n!.

Положим 0!=1.

Число 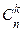= 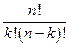– "це из n по k " – называется биномиальным коэффициентом. Отметим два свойства биномиальных коэффициентов:

= , + = .

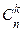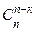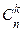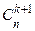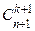Методом математической индукции, учитывая вышеприведенные формулы, можно доказать формулу бинома Ньютона

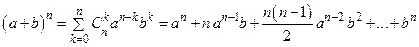. (13.2)

Дата добавления: 2015-07-20