Структура решения однородной системы.

Рассмотрим однородную систему линейных уравнений

(11.17)

или в матричной форме:

А = . (11.18)

Эта система совместна, т.к. имеет тривиальное решение х ₁ = х ₂ = …= x_n = 0.

Свойства решений однородной системы (11.17).

1. Если ₁ и ₂- решения однородной системы (11.17), или, что тоже самое, системы (11.18), то их сумма ₁+ ₂ тоже решение этой системы.

Действительно, если ₁, ₂ – решение системы (11.17), то А ₁= и А ₂= . Тогда по свойствам умножения матриц А ( ₁+ ₂)= А ₁+ А ₂= + = , т.е. ₁+ ₂ – решение однородной системы.

2. Если - решение однородной системы (11.17), а λ R, λ – тоже решение однородной системы (11.17).

Действительно, если – решение, то А =0, тогда А (λ ) = λ(А ) = λ• = , т.е. λ – решение однородной системы.

Из этих свойств вытекает, что линейная комбинация решений однородной системы линейных уравнений является решением этой системы.

Обозначим через L множество всех решений однородной системы (11.17), оно, ввиду выполнения свойств 1 и 2, называется пространством решений этой системы.

Найдем структуру решения однородной системы.

Пусть ранг матрицы А системы (11.17) равен r: P (A)= r, а М 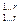- базисный минор. Тогда система (11.17) приводится к виду (см. (11.16)).

(11.19)

где х ₁, …, x_r - базисные переменные, а x_{r+ 1}, …, x_n - свободные переменные. Общее решение (11.19) системы (11.17) можно записать в виде

₀₀ = (11.20)

где ₀₀ - общее решение однородной системы, а с_{r+ 1}, …, с_n - числовые параметры. Полагая один из этих параметров равным единице, а остальные нулю, мы получим систему из n - r решений системы, называемую фундаментальной системой решений однородной системы уравнений:

_{r+ 1}= , _{r+ 2}= , _n= (11.21)

Ранг этой системы векторов равен n-r (см. выделенный минор в (11.21)), т.е. числу векторов этой системы. Поэтому эта система решений линейно независима и образует базис в пространстве решений, т.е. любое решение однородной системы является линейной комбинацией векторов фундаментальной системы решений (11.21):

₀₀ = с_{r +1 r +1} с_{r +2 r +2}+…+ с_{n n} (11.22)

Разложение (11.22) есть векторная запись формул (11.20).

Дата добавления: 2015-07-20