Умножение матриц.

Рассмотрим две матрицы и 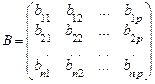размеров и соответственно, т.е. число столбцов матрицы А равно числу строк матрицы В.

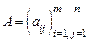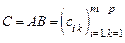Произведением матрицы на матрицу называется матрица размера , где

, (10.3)

i= 1, 2, …, m, k= 1, 2, …, p.

Другими словами, элемент с_jk матрицы С=АВ равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы к- го столбца матрицы В, т.е. равен скалярному произведению i -ой вектор- строки А_i= (а_{i 1} а_{i 2}, …, а_in) матрицы А на к -й вектор- столбец В^к = матрицы В: с_jk = А_i*B^k. Схематически это выглядит так:

i

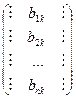
Используя запись матриц через вектор- строки и вектор- столбы, можно записать

А•В = • = .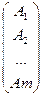

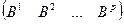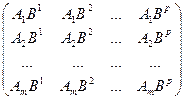Свойства умножения матриц:

1. (АВ) С=А (ВС), 2. А (В + С) =АВ+АС,

3. (А+В) С=АС+ВС, 4. (λА) В= А(λ В)= λ(АВ),

5. (АВ)^/= В^/А^/.

Пример 10.1. найти АВ и ВА, если А = 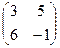В =

Решение. Обе матрицы размера 2×2, поэтому определены оба произведения: АВ и ВА.

АВ = =

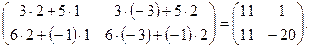
ВА=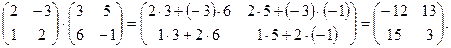

Этот пример показывает, что, вообще говоря, АВ 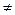ВА

Замечание. Скалярное произведение векторов с точки зрения умножения матриц.

Рассмотрим два вектора (вектор- столбца)

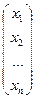= и = из Rⁿ. Тогда, учитывая замечание 1 пункта 10.1, получим

1× n

n ×1

(, )= • = = х ₁ у ₁ + х ₂ у ₂+ …+ х_nу_n = (x ₁ x ₂ … x_n) • = ^/ = ^/ .

Последнее равенство следует из того, что • = • .

Выведем свойство 5, связывающее умножение матриц с умножением, на примере матриц размера 2×2. Пусть даны две матрицы

А = 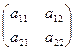= 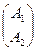, В= = ,

где А ₁, А ₂- вектор- строки матрицы А, а В¹, В ²- векторы- столбцы матрицы В. Тогда

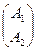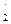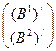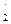АВ= (В ¹ В ²)= , (АВ ^/)= , А^/ =(А А ), В^/ = , где А , А - вектор- столбцы матрицы А^/, а , 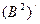- вектор- строки матрицы В^/. Найдем В^/•А^/:

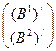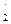В^/ А^/= •(А А )= = = (АВ) ^/.

Мы воспользовались замечанием этого пункта, из которого следует, что

(Вⁱ) ^/А = (А )^/• Вⁱ = A_j • Вⁱ, i,j= 1,2.

Дата добавления: 2015-07-20