Читайте также:
|
Пусть прямая линия l является линией пересечения двух непараллельных плоскостей α1 и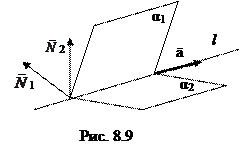 
α2 (см. рис. 8.9), заданных своими уравнениями 
и 
.
Координаты каждой точки прямой l удовлетворяют каждому из этих уравнений, т.е. системе уравнений
(8.11)
эти уравнения называются общими уравнениями прямой в пространстве.
Замечания.
1. Взаимное расположение двух прямых полностью определяется взаимным расположением их направляющих векторов.
2. Взаимное расположение прямой и плоскости в пространстве полностью определяется взаимным расположением направляющего вектора прямой и нормального вектора плоскости.
В качестве примера рассмотрим задачу о нахождении угла между прямой l, заданной уравнениями 
и плоскостью π, заданной уравнением Ах+By+Cz+D=0.
Обозначим через α острый угол между прямой l и плоскостью π, а через φ- угол между нормальным вектором 
={ А;В;С } плоскости π и направляющим вектором ā= { l,m,n } прямой l. Возможны два случая: а) угол φ- острый, б) угол φ- тупой (см. рис. 8.10).
 |
В первом случае 
Во втором случае 
Окончательно получаем формулу:
.
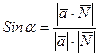Дата добавления: 2015-07-20; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение прямой, проходящей через две точки. | | | Окружность. |