Читайте также:
|
Рассмотрим в координатном пространстве Oxyz плоскость α.
Любой вектор, ортогональный данной плоскости, называется ее вектором нормали или нормальным вектором.
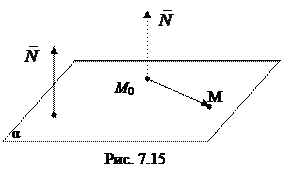Составим уравнение плоскости α, проходящей через точку 
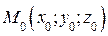ортогонально вектору 
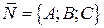(см. рис.8.1). Вектор 
есть вектор нормали плоскости α, поэтому он ортогонален любому вектору, лежащему в этой плоскости.
Рассмотрим произвольную точку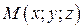 
плоскости α. Тогда векторы 
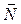и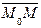 
ортогональны и их скалярное произведение равно нулю: 
. Учитывая, что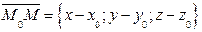 
, перепишем последнее равенство в координатной форме
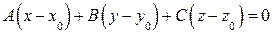(8.1)
Это и есть искомое уравнение плоскости, проходящей через данную точку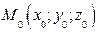 
и имеющей данный вектор нормали 
.
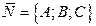Дата добавления: 2015-07-20; просмотров: 96 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрический смысл линейных неравенств и систем линейных неравенств на плоскости | | | Уравнение плоскости, проходящей через три точки. |