Уравнение прямой с угловым коэффициентом.

Рассмотрим на координатной плоскости Оху прямую l ╫ Оу, т. е. не параллельную оси Оу (см. рис. 7.2). Обозначим через φ(0≤φ<π) угол, образованный прямой с положительным направлением оси Ох. Напомним, что углы измеряются против часовой стрелки. Точка К (0, b)- точка пересечения прямой l с осью ординат Оу (см. рис. 7.2). Эти два условия однозначно определяют нашу прямую. Выведем ее уравнение. Из Δ KLN (см. рис. 7.2) ясно, что точка М(х, у) лежит на прямой l тогда и только тогда, когда

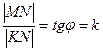, т. е.

число k=tgφ называется угловым коэффициентом прямой, а уравнение

	У=kx+b

(7.2)

называется уравнением прямой с угловым коэффициентом.

Если прямая l||Ох, т. е. φ = 0 и к = tgφ = 0, то уравнение (7.2.) принимает вид y = b.

Если прямая проходит через О(0, 0), то b = 0 и уравнение (7.2) примет вид у = кх

Если прямая l||Оу, то φ = и ее уравнение не может быть записано в виде (7.2). Пусть А (а,0) – точка пересечения прямой с осью Ох (см. рис. 7.3). Тогда точка М (х, у) лежит на прямой l тогда и только тогда, когда х = а, т..е. в этом случае уравнение прямой примет вид

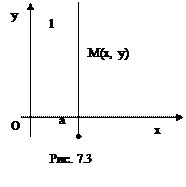х – а=0. (7.3)

В заключении отметим, что уравнения (7.2) и (7.3) есть уравнения первой степени относительно переменных х и у (координат произвольной точки прямой).

Дата добавления: 2015-07-20