Определение и свойства скалярного произведения.

Определение. Скалярным произведением векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначение: или (, ).

Если φ = (,^ ) – угол между векторами и , то

	=| | | | cosφ

(4.1)

Свойства скалярного произведения.

1. Так как | | cosφ = ПР _b , а | | cosφ = ПР _ā (см. рис. 24), то

= | | ПР _ā = | |

(4.2)

2. = вытекает непосредственно из определения.

3. (λ ) = (λ )=λ( )

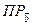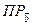
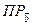
Действительно, (λ ) = | | (λ ) = | | λ = λ| | = λ( )

4. ( + ) = +

Действительно, ( + ) = | | ПР _ā( + ) = | |(ПР _ā + ПР _ā ) = | | ПР _ā +| | ПР _ā = + .

5. Скалярный квадрат вектора ² = равен квадрату его длинны: ² = | |².

Дата добавления: 2015-07-20