
Читайте также:
|
К линейным операциям над векторами относятся операция сложения векторов и операция умножения вектора на действительное число.
Сложение векторов. Под суммой векторов  и
и  понимаем вектор
понимаем вектор  +
+  , идущий из начала вектора
, идущий из начала вектора  в конец вектора
в конец вектора  , если начало вектора
, если начало вектора  приложено к концу вектора
приложено к концу вектора  (см. рис. 3.4):
(см. рис. 3.4):
 |
 Правило параллелограмма сложения векторов (см. рис. 3.5): начала векторов
Правило параллелограмма сложения векторов (см. рис. 3.5): начала векторов  и
и  совмещают, тогда сумма векторов
совмещают, тогда сумма векторов  и
и  изображается диагональю параллелограмма, построенного на векторах как на сторонах.
изображается диагональю параллелограмма, построенного на векторах как на сторонах.
Эквивалентность этих определений ясна из рис. 3.4 и 3.5.
Свойства сложения векторов:
1. Коммутативность:  +
+  =
=  +
+ 
2. Ассоциативность: ( +
+  )+
)+  =
=  +(
+( +
+  )
)
3. Нулевой вектор: существует нулевой вектор  , такой, что для любого вектора
, такой, что для любого вектора 
 +
+  =
=  +
+  =
= 
4.
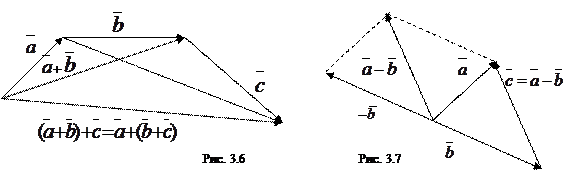 |
 существует противоположный вектор -
существует противоположный вектор -  такой, что
такой, что  +(-
+(-  )=(-
)=(-  )+
)+  =
= 
Доказательство: Свойство 1 вытекает непосредственно из определения сложения векторов по правилу параллелограмма (см. рис. 3.5). Свойство 2 вытекает из правила треугольников (см. рис. 3.6).
 Разностью векторов
Разностью векторов  и
и  называется вектор
называется вектор  –
–  =
=  +(-
+(-  ). Другими словами, разность векторов
). Другими словами, разность векторов  и
и  – это такой вектор
– это такой вектор  =
=  –
–  , который, будучи прибавлен к вектору
, который, будучи прибавлен к вектору  , даст вектор
, даст вектор  (см. рис. 3.7).
(см. рис. 3.7).
Умножение вектора на число. Произведением вектора  на число λ называется вектор λ
на число λ называется вектор λ  такой, что:
такой, что:
1.  ;
;
2.  , если λ>0;
, если λ>0;
 , если λ<0;
, если λ<0;
Свойства умножения вектора на число:
1. 1•  =
=  ;
;
2. α (β  )=(α β)
)=(α β) 
3. (α+β)  =α
=α  +β
+β 
4. 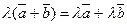
 Доказательство свойств 1, 2, 3 легко получить непосредственно из определения умножения вектора на число и сложения векторов (представляется читателю). Свойство 4 основано на подобии параллелограммов изображенных на рис. 3.9, где λ является коэффициентом подобия при λ>0.
Доказательство свойств 1, 2, 3 легко получить непосредственно из определения умножения вектора на число и сложения векторов (представляется читателю). Свойство 4 основано на подобии параллелограммов изображенных на рис. 3.9, где λ является коэффициентом подобия при λ>0.
Следствия определения и свойств линейных операций над векторами.
1. 0•  =
=  для любого вектора
для любого вектора 
2. -  =(-1)•
=(-1)• 
3. 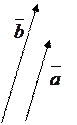 Условия коллинеарности:
Условия коллинеарности:
 ||
||  ó существует число α такое, что
ó существует число α такое, что  =α
=α  . Действительно, если
. Действительно, если  =α
=α  , то
, то  ||
||  по определению умножения вектора на число.
по определению умножения вектора на число.
Обратно. Если  ||
||  , то возможны два случая:
, то возможны два случая:
1) 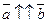 , тогда
, тогда  =α
=α  , где
, где  ,
,
2) 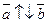 , тогда
, тогда  =α
=α  , где
, где 
4. Орт вектора:  ,
, 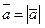 •
• 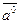 .
.
Линейная комбинация векторов. Линейной комбинацией векторов  1,
1,  2, …,
2, …,  n с коэффициентами λ1, λ2, …, λn называется вектор λ1
n с коэффициентами λ1, λ2, …, λn называется вектор λ1  1+λ2
1+λ2  2+…+λn
2+…+λn  n.
n.
Дата добавления: 2015-07-20; просмотров: 89 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторы на плоскости и в пространстве. | | | Координаты вектора в данном базисе. |