Читайте также:
|
Определение. Смешанным произведением векторов 
, 
, 
(в таком порядке) называется число
=( 
) .
Геометрический смысл смешанного произведения.
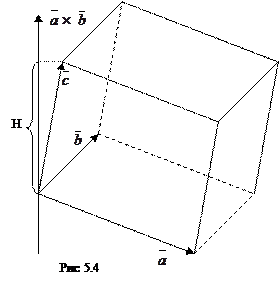Рассмотрим параллелепипед, построенный на векторах , , как на ребрах. Из рис. 5.4 ясно, что
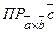= ±Н,
где Н – высота параллелепипеда, при этом берется знак “+”, если тройка , , – правая, и знак “–”, если тройка – левая.
Поэтому
= ( ) = | | 
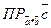= Sпар• (±Н) = ±Vпар.
Отсюда получим, что модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах как на ребрах:
Vпар=| |. (5.4)
Итак, смешанное произведение позволяет вычислить объемы параллелепипеда, призмы, тетраэдра.
Из этого свойства смешанного произведения получаем:
, , – компланарны ó = 0.
Дата добавления: 2015-07-20; просмотров: 51 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства векторного произведения | | | Определение линейного пространства. |