Общее уравнение прямой.

Общее уравнение прямой на плоскости представляет собой уравнение первой степени относительно переменных х и у, т. е. линейное уравнение

	Ах+Ву+С=0

(7.7)

Из уравнений (7.2) и (7.3) пункта 7.2.1 вытекает, что уравнение любой прямой может быть записано в виде (7.7).

Обратно, покажем, что уравнение (7.7) задает прямую на плоскости. Действительно, если В≠0, то уравнение (7.7) можно привести к виду (7.2)

, где к= – .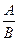

Если же В=0, то его можно привести к виду (7.3)

,

т. к. при В=0 обязательно А≠0.

Неполные уравнения прямой:

1) если А=0, то прямая параллельна оси Ох;

2) если В=0, то прямая параллельна оси Оу;

3) если С=0, то прямая проходит через начало координат О (0, 0).

Дата добавления: 2015-07-20