Читайте также:
|
Составим уравнение плоскости α, проходящей через три данные точки 
, 
и 
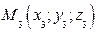, не лежащие на одной прямой.
Рассмотрим произвольную точку М(х, у, z) плоскости α. Тогда три вектора 
, 
и 
лежат в одной плоскости, т.е. компланарны (см. рис. 8.2). Следовательно, их смешанное произведение равно нулю: 
.
Заметив, что ={ х-х 1; у -у1; z-z 1 },
={ х 2 -х 1; у 2-у1; z2 -z1}, 
{ х 3 -х 1; у 3-у1; z3 -z1}, перепишем последнее равенство в координатной форме, получим уравнение плоскости, проходящей чрез три заданные точки:
(8.2)
Пусть плоскость α отсекает на координатных осях Ох, Оу, Oz отрезки a, b, и с соответственно. Тогда плоскость α проходит через три точки М 1(а;0;0), М 2(0; b;0) М 3(0;0; с). Подставив координаты этих точек в уравнение (8.2), получим уравнение плоскости в отрезках на осях
. (8.3)
Дата добавления: 2015-07-20; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение плоскости, проходящей через данную точку ортогонально данному вектору. | | | Общее уравнение плоскости. |