Точка пересечения двух прямых.

Пусть даны две прямые l ₁: А ₁ х+В ₁ у+С ₁ =0 и l ₂: А ₂ х+В ₂ у+С ₂ =0. Координаты точки пересечения этих прямых удовлетворяют одновременно обоим уравнениям, т.е. системе двух линейных уравнений с двумя неизвестными

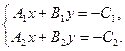(7.15)

Если определитель этой системы отличен от нуля Δ= ≠ 0, т.е. , то эта система имеет единственное решение, которое можно найти по формулам Крамера.

Условие параллельности прямых: l ₁|| l ₂ ó Δ= 0 ó (пропорциональность коэффициентов при переменных или, что тоже самое, коллинеарность векторов нормали этих прямых, см. рис. 7.12 б).

Если же = 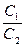, то прямые совпадают (см. рис. 7.12).

Условие ортогональности прямых (см. рис. 7.12 в):

l ₁ l ₂ ó ₁={ А ₁, В ₁} ₂={ А ₂, В ₂} ó ₁* ₂= 0, т.е. А₁ А₂+ В ₁ В ₂ =0.

Дата добавления: 2015-07-20