Нормальное уравнение прямой.

Пусть ⁰={ Cos α, Cos β } – нормальный вектор прямой, идущий о начала координат к прямой, Cos α, Cos β – направляющие косинусы вектора ⁰, | ⁰| = 1; р – расстояние от начала координат до прямой (см. рис. 7.9).

Точка М (х, у) лежит на прямой тогда и только тогда, когда 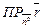= р, где = { х, у }-

х сos α + у sin α – р = 0

радиус-вектор точки М (х, у), т. е. • ⁰ = р, или в координатной форме хCos α + уCos β – р = 0. Учитывая, что Cos β = Sin α (см. рис. 7.9), получим окончательно

(7.12)

Это и есть нормальное уравнение прямой.

Для получения нормального уравнения прямой нужно умножить общее уравнение (7.7) на нормирующий множитель , где знак μ выбирается противоположным знаку С в общем уравнении Ах+Ву+С=0.

Дата добавления: 2015-07-20