Угол между прямыми. Условия параллельности и ортогональности.

Пусть даны прямые l ₁: у=к ₁ х+b ₁ и l ₂: у=к ₂ х+b ₂. Найдем угол μ между этими прямыми (измеряется от L ₁ к L ₂ против часовой стрелки) (см. рис. 7.10). Заметим, что k ₁ = tg α ₁, k ₂ = tg α ₂ и φ=α ₂ -α ₁. Если φ ≠ , то C= tg (α ₂- α ₁ ) = или

(7.13)

Условия параллельности двух прямых:,

к _{1 =} к ₂

к _{1 *} к ₂= –1

т.е. параллельных прямых означает равенство их угловых коэффициентов. Действительно, из формулы (7.13) следует, что l ₁|| l ₂ ó φ = 0, т.е. tg φ=0 ó k ₂ -k ₁=0, т.е. k ₂ =k ₁.

Условия ортогональности двух прямых:

,

т.е. к ₂= – 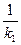. Действительно, l ₁ l ₂ ó φ = , т.е. ctg φ=0 ó = 0 ó 1+ к ₁ к ₂= 0, т.е. к ₁ к ₂= –1.

Дата добавления: 2015-07-20