Нормальное уравнение плоскости.

Составим уравнение плоскости α, проходящей на расстоянии р от начала координат ортогонально единичному вектору ⁰, идущему от начала координат О к плоскости α (см. рис. 8.4). Координатами вектора ⁰сужат его направляющие косинусы, поэтому ⁰={ Cos α, Cos β, Cos γ}.

x

Если точка М (х; y; z) лежит в плоскости α, то проекция вектора = ={ х; y; z } на орт ⁰

равна р: = р, что можно переписать в виде р.

Записав это уравнение в координатной форме, получим нормальное уравнение плоскости

p =0. (8.5)

Чтобы получить нормальное уравнение плоскости, нужно общее уравнение плоскости (8.4) умножить на нормирующий множитель 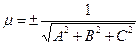, где знак выбирается противоположным знаку D в общем уравнении плоскости Ах+Ву+Сz+D=0.

Дата добавления: 2015-07-20