Квадратные матрицы. Обратная матрица.

Квадратнойматрицейпорядка n называется матрица размера n×n, т.е. число строк матрицы равно числу ее столбцов:

А= 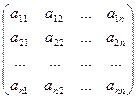. (10.4)

Элементы а ₁₁, а ₂₂, …, а_nn образуют главную диагональ матрицы А =(а_ij) , .

Транспонирование квадратной матрицы сводится к зеркальному отражению относительно главной диагонали.

Через | А | = ∆ = det A обозначим определитель квадратной матрицы А:

∆ = det A = .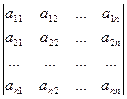

Квадратная матрица А называется невырожденной, если ее определитель не равен нулю: ∆= det A ¹ 0, и вырожденной, если ее определитель равен нулю: ∆= det A = 0

Единичной матрицей порядка n называется квадратная матрица Е_n, у которой элементы главной диагонали равны единице, а все остальные элементы равны нулю:

а_ij =1, i =1, …, n, а_ij =0 при i≠j, т.е.

Е_n= .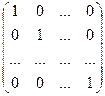

Единичная матрица Е_n обладает свойством: для любой квадратной матрицы А порядка n

АЕ_n=Е_nА=А,

т.е. эта матрица играет при умножении матриц ту же роль, что и число 1 при умножении чисел.

Заметим без доказательства, что det (AB)= det A • det B. (10.5)

Матрица А^{- 1} называется обратной к матрице А, если

А^{- 1} • A = A • А^{- 1} = Е_п, (10.6)

где А^{- 1} и А - матрицы порядка n. Из определения ясно, что матрицы А^{- 1} и А взаимно обратны: матрица А является обратной к матрице А^{- 1}.

	Всякая невырожденная матрица имеет обратную.

Свойства обратной матрицы:

1. det А^{- 1}= ;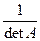

2. (АВ) ^{- 1}= В^{- 1} А^{- 1};

3. (А^{- 1})^/=(А^/)^-1.

Свойство 1 вытекает из формул (10.5) и (10.6):

1= det Е_n = det (А•А^{- 1})= det A• det A ^-1.

Свойство 2 вытекает из равенства (10.6):

Е_n = Е 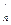=(А•А^{- 1})^/= (А^{- 1})^/ • А^/,

т.е. по определению (А^/)^-1= (А^{- 1})^/.

Нахождение обратной матрицы.

1. Если матрица А =(а_ij) 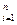, 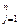порядка n невырождена, det A≠0, то обратная к ней матрица А^{- 1} имеет вид:

А^{- 1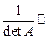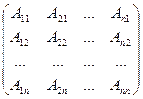}= , (10.7)

Где А_ij - алгебраическое дополнение элемента а_ij матрицы А, ij =1, …, n. Алгебраические дополнения элементов матрицы определяется так же, как и алгебраические дополнения элементов определителя.

Пример 10.2. Найти обратную матрицу А^{- 1}, если

А = .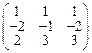

Решение. Так как 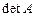= =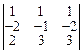-3-6-4-(-2-6-6)=1, то матрица А имеет обратную. Найдем алгебраические дополнения к элементам матрицы А.

; ; ;

; ; ;

; ; .

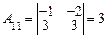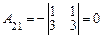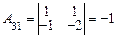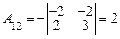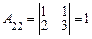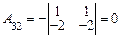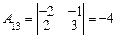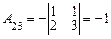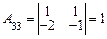Тогда .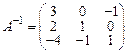

Проверка: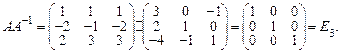

2. Нахождение обратной матрицы методом элементарных преобразований (методом Гаусса).

К элементарным преобразованиям матрицы относятся:

1) перестановка местами двух строк матрицы;

2) умножение всех элементов какой-либо строки матрицы на число, отличное от нуля;

3) прибавление к элементам одной строки матрицы соответствующих элементов другой строки, умноженных на одно и то же число.

Матрицы А и В называются эквивалентными, А~В, если одна из них получается из другой с помощью элементарных преобразований.

Припишем к невырожденной матрице А порядка п единичную матрицу Е_n, получим матрицу (А|Е_n) размера n ×2 n. С помощью элементарных преобразований строк приведем эту матрицу к виду (E_n|A ^-1), т.е.

(А|Е_n)~(E_n|A ^-1).

Пример 10.3. Найти А ^-1 с помощью элементарных преобразований, если А= .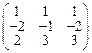

Решение. Обозначим через c_i i -ю строку матрицы А. Тогда, применяя элементарные преобразования, получим:

с ₁- с ₃

с ₃- с ₂ с ₁- с ₂

с ₂+2 с ₁ с ₃-2 с ₁

(A|E ₃)= ~ ~ ~

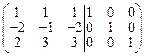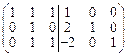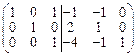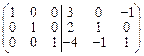~ =(E ₃| A ^-1)

Итак,

А ^-1= .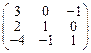

Дата добавления: 2015-07-20