Парабола.

Пусть на плоскости заданы прямая l и точка F, отстоящая от этой прямой на расстоянии p ().

Параболой называется множество всех точек плоскости, каждая из которых равноудалена от данной точки F, называемой фокусом, и данной прямой l, называемой директрисой.

Для получения уравнения параболы введем систему координат Oxy так, как показано на рис. 9.10.

Фокус F получит координаты , уравнение директрисы l имеет вид . Каждая точка параболы М (х,у) удовлетворяет условию: , где , .

Тогда ее уравнение примет вид .

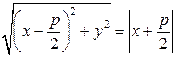Возведем обе части этого равенства в квадрат:

.

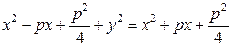Окончательно получим каноническое уравнение параболы

. (9.11)

Число p называется параметром параболы и характеризует ее форму: чем меньше p, тем сильнее ветви параболы прижимаются к оси Ох.

Если вершина параболы находится в точке , а осью симметрии является прямая 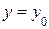, то уравнение параболы примет вид (см. рис. 9.11)

(9.12)

В заключение приведем некоторые частные уравнения парабол (см. рис. 9.12).

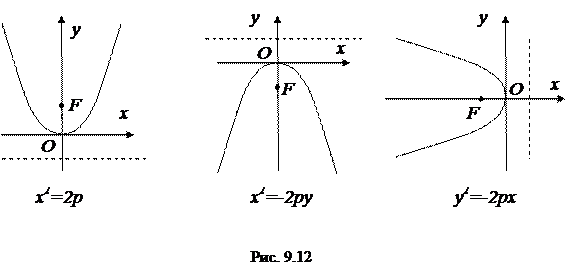Дата добавления: 2015-07-20