Матрицы

Основные понятия

Матрицей размера m×n называется прямоугольная таблица чисел вида

А=(а_ij) = (10.1)

содержащая т строк и п столбцов. Числа а _ij называются элементами матрицы; индекс i – номер строки, в которой стоит данный элемент, i = 1,2,..., т, а j – номер столбца, j – 1,2,..., п.

Равенство матриц. Две матрицы А=(а_ij) и В=(b_ij) одинакового размера m×n называется равными: А=В, если равны все элементы матриц, стоящие на одинаковых местах, т.е. А=В ó a_ij=b_ij, где i= 1, …, m; j= 1, …, n.

Нулевая матрица О - это матрица, все элементы которой равны нулю: a_ij=0, i= 1, …, m; j= 1, …, n, т.е.

О= .

Противоположная матрица. Матрица -А= называется противоположной к матрице А=

Транспонированная матрица. Матрица размера n×m, полученная из матрицы А=(а_ij) размера m×n заменой ее строк столбцами с теми же номерами, называется транспонированной к А матрицей, т.е. (см. формулу (10.4))

А́= .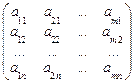

Ясно, что = А.

Обозначим через М_m×n множество всех матриц размера m×n.

Замечания. 1) Пусть =(х ₁, х ₂, …, х_n)- n - мерный вектор пространства n- мерных арифметических векторов Rⁿ. В дальнейшем мы будем рассматривать его как вектор- столбец и записывать как матрицу размера n ×1: = , а ΄=(х ₁ х ₂ … х_n)- вектор-строка, т.е. матрица размера 1× n, транспонированная к вектор-столбцу .

2) Запись матрицы с помощью ее вектор-строк и вектор-столбцов.

Пусть A_i=(a_i1 a_i2... a_in) – i- тая вектор-строка матрицы А, i = 1, 2,..., m, – j -тый вектор-столбец, j= 1, 2,..., n, тогда матрицу А можно записать в виде

. (10.2)

В частности, А' = , где – n- мерный вектор-столбец, i = 1, 2,..., m.

---

Дата добавления: 2015-07-20