Гипербола

Рассмотрим на плоскости две точки и 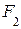, расстояние между которыми равно 2с, и число .

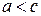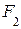Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек и , называемых фокусами, есть величина постоянная, равная , т.е.

, (9.7)

где и – фокальные радиусы произвольной точки М гиперболы (см. рис. 9.7).

Введем систему координат Oxyz точно также, как это сделано при выводе канонического уравнения эллипса в пункте 9.2 (см. рис. 9.7). Координаты фокусов 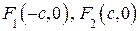и , . Подставляя эти формулы в равенство (9.7), получим

.

Упрощая это уравнение как при выводе уравнения эллипса, получим каноническое уравнение гиперболы

, (9.8)

где

. (9.9)

Уравнение (9.8) показывает, что гипербола симметрична как относительно осей координат Ох и Оу, так и относительно начала координат О(0,0) – центра гиперболы. На рис. 9.8 изображена гипербола, задаваемая уравнением (9.8), где – действительная полуось, – мнимая полуось. Пунктиром изображены основной прямоугольник гиперболы и прямые , проходящие через вершины основного прямоугольника, называемые асимптотами гиперболы. Они обладают тем свойством, что расстояния от точки гиперболы до соответствующей асимптоты стремится к нулю при неограниченном удалении точки от начала координат.

Эксцентриситет гиперболы больше единицы: , т. к. 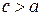. Он характеризует форму гиперболы: чем меньше эксцентриситет, тем более вытянут основной прямоугольник, т. к. .

Сопряженная гипербола, задаваемая уравнением

, (9.10)

имеет те же асимптоты , ее фокусы расположены на оси Оу, – действительная полуось, – мнимая полуось (см. рис. 9.9).

Дата добавления: 2015-07-20