Методы решения невырожденных СЛАУ.

Рассмотрим n уравнений с n неизвестными

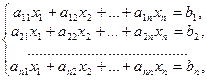(11.6)

или в матричной форме

А = , (11.7)

Где матрица А - квадратная матрица порядка n. Определитель этой матрицы
Δ = det A=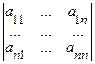

называется определителем системы. Если det A ≠0, система (11.6) называется невырожденной (матрица системы А - невырожденная матрица).

а) Матричный метод решения системы

Если Δ= det A ≠0, то матрица А имеет обратную А ^-1. Умножив обе части уравнения (11.7) слева на матрицу А ^-1, получим А ^-1 А = А^{- 1} , т.к. А ^-1 А=Е, то окончательно получаем

= А^{- 1}

(11.8)

б) Формулы Крамера.

Перепишем равенство (11.8) в виде

= ,

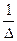
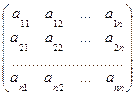
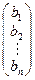или

х ₁ = 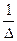(b ₁ A ₁₁ +b ₂ A ₂₁+…+ b_nA_{n 1}),

х ₂ = 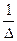(b ₁ A ₁₂ +b ₂ A ₂₂+…+ b_nA_{n 2}),

………………………………..

х_n= 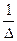(b ₁ A _{1 n} +b ₂ A _{2 n} +…+ b_nA_nn).

Заметим, что

Δ₁= 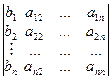= b ₁ A ₁₁ +b ₂ A ₂₁+…+ b_nA_{n 1},

Δ₂= 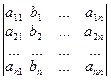= b ₁ A ₁₂ +b ₂ A ₂₂+…+ b_nA_{n 2},

Δ _п = 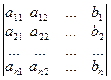= b ₁ A _{1 n} +b ₂ A _{2 n} +…+ b_nA_nn.

Окончательно, х ₁= 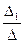, х ₂= 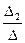, …, х_n = .

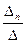Формулы Крамера:

	хi = , i =1, 2, …, n

(11.9)

где Δ- определитель системы, а определитель Δ _i, i = 1, …, n получается из определителя Δ заменой i- го столбца столбцом свободных членов.

Итак, невырожденная система совместна и имеет единственное решение, которое может быть найдено или по формуле (11.8) или по формулам Крамера (11.9).

Дата добавления: 2015-07-20