Множества. Действия над множествами.

Понятие множества является одним из основных понятий математики и не поддается точному определению. Под множеством мы понимаем совокупность каких-либо объектов, объединенных по какому-нибудь признаку.

Говоря о множестве, мы имеем ввиду следующее:

1) множество состоит из любых различимых объектов;

2) множество однозначно определяется набором составляющих его объектов;

3) любое свойство определяет множество объектов, обладающих этим свойством.

Множества будем обозначать большими буквами латинского алфавита, а объекты, их составляющие, малыми буквами.

Пусть X – множество, х – объект, P – свойство. Тогда запись P(x) означает, что объект х обладает свойством P, а запись

,

читается "множество объектов х таких, что Р(х) ", означает множество Х объектов х, обладающих свойством Р. Еще раз отметим, что любое свойство Р однозначно определяет множество объектов, этим свойством обладающих.

Объекты х, составляющие множество Х, называются его элементами. Если х – элемент множества Х, то пишем х Î Х, т.е. элемент х принадлежит множеству Х, и х Ï Х, если х не является элементом множества Х (не принадлежит множеству Х).

Равенство множеств. Два множества А и В равны, А = В, если они состоят из одних и тех же элементов, т.е. (хÎА) Û (хÎВ).

Подмножество, включение. Множество А называется подмножеством (частью) множества В, если каждый элемент множества А является элементом множества В.

Пишем А Ì В, читаем " А вложено (включено) в В ".

Таким образом, А Ì В означает, что(хÎА) Þ (хÎВ).

На языке включения равенство множеств можно записать следующим образом:

(А = В) Û (А Ì В) 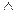(В Ì А).

Пустое множество – множество, не содержащее элементов; обозначается символом Æ и является подмножеством любого множества.

Действия над множествами. Далее считаем, что все рассматриваемые множества являются подмножествами некоторого множества М.

Объединением (суммой) множеств А и В называется множество А В (или А + В), состоящее из элементов, принадлежащих или множеству А, или множеству В (хотя бы одному из них):

А В =

Пересечением (произведением) множеств А и В называется множество А В (или А В), состоящее из элементов, принадлежащих как множеству А,, так и множеству В (одновременно двум множествам):

А В =

Разностью множеств А и В называется множество А \В, состоящее из элементов множества А, не принадлежащих множеству В:

А \В =

Дополнением множества А (до множества М) называется множество = М \А, состоящее из тех элементов множества М, которые не принадлежат множеству А:

= М \А =

Заметим, что А = Æ и А + = М.

Законы двойственности. Для любых множеств А Ì М и В Ì М справедливы равенства

, .

Докажем первое из этих равенств. Нужно показать, что каждый элемент множества 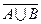является элементом множества и наоборот:

.

Аналогично доказывается второе равенство. Предоставляем это сделать читателю.

В заключение поясним введенные понятия диаграммами. Множества будут изображаться множествами точек плоскости, элементы множеств – точками плоскости. Тогда (см. рис. 13.1)

		Рис. 13.1.

Дата добавления: 2015-07-20