|
Читайте также: |
Дополним числовую прямую двумя символами ±¥, называемыми бесконечно удаленными точками, при этом 
х Î R -¥< x <+¥. Тогда множество действительных чисел можно записать в виде
R= (-¥, +¥)={ x: -¥< x <+¥}.
Пусть a и b - действительные числа, и пусть a < b.
Числовыми промежутками называем подмножества множества действительных чисел R вида:
[ a, b ]={ x Î R: a ≤ x ≤ b }- отрезок (сегмент, замкнутый промежуток);
(a, b)={ x Î R: a < x,< b }- интервал (открытый промежуток);
[ a, b)={ x Î R: a ≤ x < b },
(a, b ]={ x Î R: a < x ≤ b }- полуинтервалы;
(-¥, b ]={ x Î R: х ≤ а },
[ а, + ¥)={ x Î R: х ³ а }- полупрямые;
(-¥, а)={ x Î R: х < а },
(а, + ¥)={ x Î R: х > а }- открытые полупрямые.
Длина отрезка I =[ a, b ] по определению считается равной | I | = |[ a, b ]|= b-a.
Окрестностью действительного числа (точки числовой прямой) называется любой интервал, содержащий эту точку (см. рис. 13.3 а).
Интервал U (x 0, ε)={ x Î R: x 0- ε < x < x 0+ ε } с центром в точке х 0 и радиуса ε называется ε -окрестностью точки х 0 (см. рис. 13.3 б).
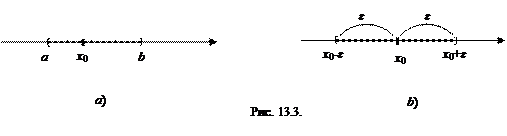
Неравенство х 0- ε < x < x 0+ ε или, что тоже самое, | x-x 0|< ε, означает, что х Î{ x 0- ε, x 0+ ε }, т.е.
U (x 0, ε)= { x Î R: |x - x 0|< ε }.
Замечание. Подчеркнем, что символы +¥ и -¥ не числа. Они символизируют процесс неограниченного удаления точек числовой прямой вправо и влево от нуля.
Пример 13.1. Рассмотрим полуинтервал Х= [0, 1). Это ограниченное множество, т.к. х Î Х 0£ х <1, где 0 – нижняя, а 1 – верхняя границы множества Х. Ясно, что 0= inf X= min X, 1= sup X, т.е. число 0 является как нижней границей множества Х, так и наименьшим элементом этого множества. Число 1 является точной верхней границей нашего множества, наибольшего элемента оно имеет:
Дата добавления: 2015-07-20; просмотров: 178 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ограниченные и неограниченные числовые множества. | | | Индуктивные множества. Натуральные числа. Метод математической индукции. |