Читайте также:
|
Если каждому натуральному числу nÎN поставить в соответствие действительное число 
, то говорим, что задана последовательностьдействительныхчисел
, (14.1)
другими словами, последовательность – это функция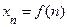 
, определенная на множестве натуральных чисел N со значениями во множестве действительных чисел R; 
.
Последовательность (14.1) будем обозначать одним из символов: 
, 
или 
, 
.
Числа 
называются членами последовательности, – общий или n-тыйчленпоследовательности.
Формула 
, выражающая общий член последовательности через его номер n, называется формулой общего члена последовательности.
Замечания. 1) Последовательность как функцию натурального аргумента можно представить следующим образом:
,
или как вектор с бесконечным числом координат.
2) Не путать последовательность (как функцию) с множеством тех значений, которые эта последовательность принимает.
Пример 14.1. 1) Рассмотрим последовательность , где 
– формула общего члена последовательности
-1, 1, -1,..., (-1) n,
Множество значений этой последовательности состоит из двух чисел 
.
2) , 
: 
3) 
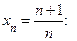
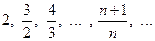
4) Постоянная последовательность 
, С, С,... С,...
5) Последовательность десятичных приближений числа 
:
|
0,3; 0,33, 0333,..., 0,33... 3;....
Дата добавления: 2015-07-20; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Индуктивные множества. Натуральные числа. Метод математической индукции. | | | Геометрическая прогрессия |