
Читайте также:
|
Переходим к центральному понятию данного параграфа.
Число а называется пределом числовой последовательности  , если для любого положительного числа ε существует такое натуральное число n 0Î N, что для всех номеров n > n 0 выполняется неравенство
, если для любого положительного числа ε существует такое натуральное число n 0Î N, что для всех номеров n > n 0 выполняется неравенство
| xn - a |< ε.
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Обозначение:  xn = a или
xn = a или  .
.
В логической символике определение предела последовательности выглядит так:
|


Поэтому определение предела последовательности можно сформулировать так:
Число а называется пределом последовательности { xn }, если для любой ε –окрестности U(a, ε) точки а существует номер n 0Î N такой, что для всех номеров n > n 0 все члены последовательности xn попадут в эту окрестность:
xn Î U(a, ε).
Заметим, что чем меньше ε, тем больше номер n 0, но в любом случае в ε –окрестность точки а попадают все члены последовательности, начиная с некоторого номера (n > n 0), а вне этой окрестности находится не более конечного числа членов. Рассмотрим ε 2< ε 1.
Пусть  xn = а, тогда (см. рис. 14.2.)
xn = а, тогда (см. рис. 14.2.)
для ε 1>0  n 1
n 1  n > n 1 xn ÎU (a 1, ε 1),
n > n 1 xn ÎU (a 1, ε 1),
для ε 2>0  n 2, в.ч. n 2> n 1,
n 2, в.ч. n 2> n 1,  n > n 2 xn ÎU (a 1, ε 2),
n > n 2 xn ÎU (a 1, ε 2),
 x 1, x 2, …, xn 1, xn 1+1, …, xn 2, xn 2+1, …, xn, …
x 1, x 2, …, xn 1, xn 1+1, …, xn 2, xn 2+1, …, xn, …
Рассмотрим примеры.
Пример 14.3. Рассмотрим последовательность { xn } с общим членом xn = 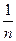 : 1,
: 1, 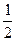 ,
, 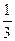 ,…,
,…, 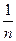 ,...
,...
Покажем, что  xn =
xn = 
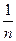 = 0. По определению, число а = 0 будет пределом последовательности xn =
= 0. По определению, число а = 0 будет пределом последовательности xn =  , если
, если  ε >0
ε >0  n 0Î N такое, что
n 0Î N такое, что  n > n 0 выполняется неравенство |
n > n 0 выполняется неравенство | 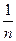 -0|< ε, т.е.
-0|< ε, т.е. 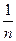 < ε. Это неравенство справедливо для всех n >
< ε. Это неравенство справедливо для всех n > 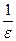 , т.е. для всех n > n 0 =
, т.е. для всех n > n 0 =  , где
, где  - целая часть числа
- целая часть числа 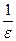 . Итак, для
. Итак, для  ε >0 найден соответствующий номер n 0, т.е. по определению
ε >0 найден соответствующий номер n 0, т.е. по определению 
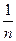 =0.
=0.
Пример 14.4. xn =  , | q |>1. покажем что
, | q |>1. покажем что 
 =0.
=0.
Действительно  < ε ó
< ε ó 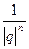 < ε ó | q | n >
< ε ó | q | n > 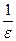 ó n > log| q |
ó n > log| q | 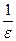 ,
,
т.е.  ε >0
ε >0  n 0=
n 0= 
 n > n 0 выполняется указанная цепочка неравенств, доказывающая утверждение.
n > n 0 выполняется указанная цепочка неравенств, доказывающая утверждение.
Аналогично, если xn = qn, | q |<1, то  qn =0.
qn =0.
Пример 14.5. Рассмотрим постоянную последовательность { xn } с общим членом xn = c, n Î N, где с = const – постоянная. Покажем, что эта последовательность сходится и  xn = c (предел константы равен самой константе).
xn = c (предел константы равен самой константе).
Действительно,  ε >0
ε >0  n | xn-c |=| c-c |=0< ε, что и требовалось доказать.
n | xn-c |=| c-c |=0< ε, что и требовалось доказать.
Пример 14.6. Покажем, что последовательность { xn } с общим членом xn =(-1) n расходится. Для этого воспользуемся вторым, геометрическим определением предела последовательности. Если а ≠ ±1, то число а не является пределом нашей последовательности, т.к. существует такая окрестность числа а, в которой нет ни одного члена рассматриваемой последовательности (см. рис 14.3а)
 Если а = 1, то в указанную окрестность точки 1 (ε =1), не попадут все члены последовательности с нечетными номерами x 2 n +1=(-1)2 n +1 = -1 (см. рис. 14.3б). Аналогично показывается, что число а = -1 не является пределом рассматриваемой последовательности, т.е. последовательность xn =(-1) n предела не имеет и расходится.
Если а = 1, то в указанную окрестность точки 1 (ε =1), не попадут все члены последовательности с нечетными номерами x 2 n +1=(-1)2 n +1 = -1 (см. рис. 14.3б). Аналогично показывается, что число а = -1 не является пределом рассматриваемой последовательности, т.е. последовательность xn =(-1) n предела не имеет и расходится.
Пример 14.7. Покажем, что 
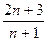 =2, и найдем номер n 0 для ε =0,1; ε =0,01 ε =0,001.
=2, и найдем номер n 0 для ε =0,1; ε =0,01 ε =0,001.
Покажем, что  ε >0
ε >0  n 0
n 0  n > n 0
n > n 0  < ε.
< ε.
Решая последнее неравенство, получим
 < ε ó
< ε ó  < ε ó n +1 >
< ε ó n +1 > 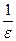 ó n >
ó n > 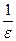 -1.
-1.
Положив n 0=  , получим, что это неравенство выполняется для всех n > n 0. Ответ на второй вопрос дает нижеприведенная таблица:
, получим, что это неравенство выполняется для всех n > n 0. Ответ на второй вопрос дает нижеприведенная таблица:
| ε | 0,1 | 0,01 | 0,001 |
| n 0 |
Если ε= 0,1, то неравенство  выполняется при
выполняется при  ; если ε= 0,01, то это неравенство выполняется при
; если ε= 0,01, то это неравенство выполняется при  и т.д.
и т.д.
Из определения предела последовательности вытекают следующие свойства сходящихся последовательностей.
Теорема 14.1. 1) Сходящаяся последовательность имеет только один предел.
2) Сходящаяся последовательность ограничена.
Доказательство. 1) Рассмотрим сходящуюся последовательность  , имеющую два различных предела a и b, a
, имеющую два различных предела a и b, a 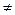 b. Пусть, например, a < b. Покажем, что такое предположение ведет к противоречию. Действительно,
b. Пусть, например, a < b. Покажем, что такое предположение ведет к противоречию. Действительно,  ,
,
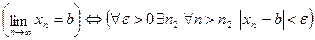 .
.
Выберем ε=  (см. рис. 14.4), положим n0=
(см. рис. 14.4), положим n0=  .
.
 |
Тогда для выбранного ε и всех n>n0 выполняются одновременно оба неравенства:
a-ε < xn < a+ε и b-ε < xn <b+ε,
т.е. xn < a+ε < b-ε < xn, что невозможно. Это противоречие исчезает, если a = b.
2) Пусть  сходится и
сходится и  xn=a. Покажем, что последовательность ограничена. Воспользуемся опять определением предела последовательности: для ε =1
xn=a. Покажем, что последовательность ограничена. Воспользуемся опять определением предела последовательности: для ε =1  n0
n0  n>n0
n>n0  . Отсюда
. Отсюда  n>n0
n>n0  .
.
Пусть А= 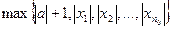 . Тогда
. Тогда  ≤А
≤А  nÎN, что и означает ограниченность последовательности.
nÎN, что и означает ограниченность последовательности.
Теорема доказана полностью.
В заключение этого пункта отметим, что из ограниченности последовательности не вытекает ее сходимость. Действительно, последовательность xn = (-1)n ограничена,  ≤1, но,, как показано в примере 14.5, она расходится.
≤1, но,, как показано в примере 14.5, она расходится.
Дата добавления: 2015-07-20; просмотров: 102 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ограниченные и неограниченные последовательности. | | | Бесконечно малые и бесконечно большие последовательности и их свойства. |