|
Читайте также: |
Последовательность { xn } называется ограниченной сверху, если множество ее значений ограничено сверху, т.е. существует число M Î R такое, что xn ≤ M 
n Î N.
В логической символике
({ xn } ограничена сверху) ó (
M n Î N xn ≤ M).
Последовательность { xn } называется ограниченной снизу, если множество ее значений ограничено снизу, т.е. существует число m Î R такое, что xn ³ m n Î N, или
({ xn } ограничена снизу) ó ( m n Î N m ≤ xn).
Последовательность { xn } называется ограниченной, если она ограничена сверху и снизу, т.е. существуют числа m, M Î R такие, что m ≤ xn ≤ M n Î N, или
({x п } ограничена) ó ( m, M nÎN m ≤ xn ≤ M),
или
({ xn } ограничена) ó ( А >0 n Î N |xn| ≤ A).
Последовательность, не являющаяся ограниченной (ограниченной сверху, ограниченной снизу), называется неограниченной (неограниченной сверху, неограниченной снизу):
({ xn } неограничена) ó ( А >0 n 0Î N |xn 0 | > A)
Если последовательность ограничена сверху, то все ее члены принадлежат промежутку (¥, M ], а если ограничена снизу – промежутку [ m, +¥), а в случае ограниченности – отрезку [ m,M ].
Примеры 14.2. 1) { xn }, где xn = n: 1, 2, …, n, … ограничена снизу (m =1), но не ограничена сверху (принцип Архимеда);
2) последовательность { xn }, xn =(-1) nn: -1, 2, -3, 4, … – неограниченная;
3) { xn }, xn =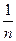 
: 1,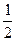 
, 
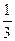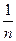, …, , … – ограничена, т.к. 0 < 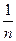≤1, 0 < xn ≤1 n Î N.
Дата добавления: 2015-07-20; просмотров: 109 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Геометрическая прогрессия | | | Определение предела последовательности. |