Ограниченные числовые множества

Определение 1. Если для числового множества P Ì R существует такое конечное число l Î R, что x £ l, для любого числа x из P, то будем говорить, что множество P ограничено сверху (справа); само число l называется верхней границей множества P.

Если множество Р ограничено сверху, то оно имеет бесконечное множество верхних границ. Действительно, любое число l ₁ >l,очевидно, так же будет верхней границей. Наименьшую верхнюю границу l ₀ множества Р называют точной верхней границей и для ее обозначения употребляется символ sup P = l ₀(supremum P). Заметим, что sup P может принадлежать, а может и не принадлежать множеству Р. Если все числа х множества Р удовлетворяют неравенству х £ l,то и sup P £ l.

Если множество Р сверху не ограничено, то за его верхнюю границу принимают “несобственное число” +∞ и записывают sup P = +∞. Относительно символа +∞ считают, что x <+∞, каково бы ни было число x из R.

Определение 2. Если для числового множества P Ì R $ b Î R такое, что x ³ b " x Î P, то будем говорить, что множество P ограничено снизу (слева); само число b называется нижней границей множества P.

Из всего множества нижних границ наибольшую b ₀ называют точной нижней границей множества P и для ее обозначения употребляется символ inf P = b ₀ (infimum P). Inf P может принадлежать, а может и не принадлежать множеству P. Если все числа x множества P удовлетворяют неравенству x ³ b,то и inf P ³ b.

Если множество P снизу не ограничено, то за его нижнюю границу принимают "несобственное число" – ∞ и записывают inf P = – ∞. Относительно символа – ∞ полагают, что х > – ∞, каково бы ни было число х из R.

Определение 3. Если числовое множество P ограничено и сверху, и снизу, то такое множество называется ограниченным.

Для любого числа х из ограниченного множества P выполняются неравенства b ₀ £ х £ l ₀, где l ₀ = sup P, а b ₀ = inf P.

Для любого ограниченного множества P существует такое число m > 0, что 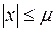для любого числа х из Р. Это неравенство можно записывать иначе:

–m £ х £ m.

Если числовое множество Р не ограничено, то все значения x Î R удовлетворяют неравенству – ∞ < х < +∞.

Примеры:

1. Р = N. Множество N натуральных чисел ограничено снизу. Inf N = 1, sup N = +∞.

2. P = { x | x = m/n, m Î N, n Î N и m < n }. Это множество правильных дробей; оно ограничено и снизу, и сверху: inf P = 0, sup P = 1, т.е. является ограниченным множеством.

3. P = R. Множество R действительных чисел является неограниченным множеством и поэтому " x Î R; имеем – ∞ < x < +∞.

Определение 4. Числовое множество, в котором числовые значения изменяются непрерывным или сплошным образом, называется числовым промежутком.

В большинстве случаев именно числовой промежуток служит областью определения числовой функции.

---

Дата добавления: 2015-07-20