Множества.

Дискретная математика.

Дискретная математика – это часть математики, занимающаяся изучением свойств структур дискретного характера. Эти структуры возникают как в самой математике, так и в ее приложениях, в том числе в экономике, кибернетике и т.д. Дискретность – антипод непрерывности. Дискретное – раздельное, состоящее из разрозненных частей.

Использование классической или дискретной математики как аппарата исследования связано с характером задач, которые рассматривает исследователь, какую модель он рассматривает дискретную или непрерывную. Например, конечное по количеству – всегда дискретно. Методы дискретной математики характеризуются необходимостью отказа от основополагающих понятий классической математики, таких как предел, производная, интеграл и т.д.

Множества.

Состав объектов исследования может быть представлен в виде дискретного множества. Множество – основное понятие в теории множеств, которое вводится без определения.

Основные понятия.

Множество состоит из элементов. Принадлежность элемента a множеству М обозначается a 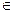M, непринадлежность – a M. Множество A называется подмножеством множества В (обозначается А В), если всякий элемент из А является элементом В.

Дата добавления: 2015-07-20