Основные свойства операций над множествами.

Некоторые свойства операций над множествами похожи на свойства алгебраических операций.

1. Свойство идемпотентности:

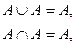
2. Свойство коммутативности операций объединения и пересечения:

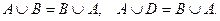
3. Свойство ассоциативности операций объединения и пересечения

4. Свойство дистрибутивности

5. Свойство поглощения

Доказательства можно провести с помощью диаграммы Венна (самостоятельно).

Число элементов конечного множества А называется его мощностью и обозначается | A |.

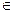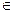Определение. Множество называется декартовым произведением множеств А, если члены этого множества состоят из упорядоченных пар (а, b), таких, что а А, b B.

Дата добавления: 2015-07-20