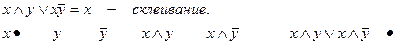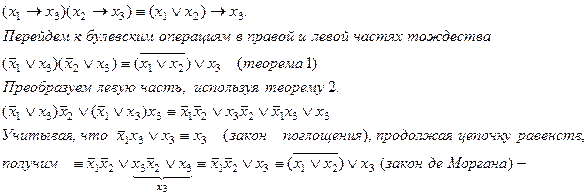Формулы алгебры высказываний.

1. Других формул алгебры высказываний нет.

Замечание: Для упрощения формул алгебры высказываний приняты следующие упрощения.

1. Наружные скобки в записи формул можно опустить.
2. Считается по определению, что конъюнкция «сильнее» дизъюнкции, а обе они «сильнее» → и ~. Поэтому часть скобок, определяющих порядок действий, можно опустить.
3. Скобки, определяющие порядок действий в ассоциативном случае можно опустить.
4. Конъюнкцию будем обозначать ∙ или опускать.

Например, упрощенная запись формулы

.

П р и м е р 1.С помощью равносильных преобразований доказать равенство: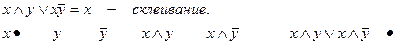

0 0 1 0 0 0

0 1 0 0 0 0

1 0 1 0 1 1

1 1 0 1 0 1

П р и м е р 2.

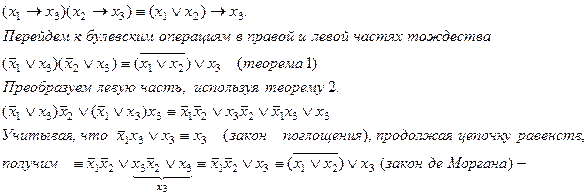
что и требовалось доказать.

Дата добавления: 2015-07-20