Примеры. В В В 1. Множество студентов ВВФ МТУСИ.

В В В 1. Множество студентов ВВФ МТУСИ.

2. Множество задач в контрольной работе.

А 3. Множество натуральных чисел.

4. Множество натуральных чисел, не превосходящих 100.

Некоторые множества имеют стандартные обозначения.

N – множество всех натуральных чисел;

Z – множество всех целых чисел;

Q – множество всех рациональных чисел;

R – множество всех действительных чисел;

C – множество всех комплексных чисел;

B = {0, 1}, это множество называется булевым отрезком.

Пусть Р – некоторое свойство, которым может обладать или не обладать элемент множества А (a 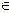A).Тогда через { a 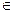A ‍│ P(a)} обозначается множество всех элементов, обладающих свойством Р.

П р и м е р. М = {n 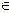N │ ⁿ /₂ 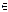N, n ≤ 100} – множество четных чисел, не превышающих 100.

Дата добавления: 2015-07-20