
Эквиваленция (равносильность) соответствует в русском языке конструкции «тогда и только тогда».
Определение.
Эквиваленцией высказываний a и b называется высказывание, обозначаемой a ~ b (a ↔ b) и определяемое следующей таблицей:




0 0 1
0 1 0
1 0 0
1 1 1
Отсюда следует, что эквиваленция истинна тогда и только тогда, когда образующие ее высказывания a и b имеют равные значения истинности.
Имеют место следующие свойства:
1. а ~ b ≡ b ~ a – коммутативность.
2. 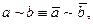
3. a ~ 1 ≡ a.
4. a ~ 0 ≡ 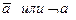
Дата добавления: 2015-07-20; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дизъюнкция. | | | Т.е. импликация ложна тогда и только тогда, когда a – истина, а b – ложь. |