|
Читайте также: |
Определение. Две формулы алгебры высказываний f1 (x1, x2,...., xn) и f2 (x1, x2,...., xn) называются равносильными (f1 (x1, x2,...., xn) ≡ f2 (x1, x2,...., xn)), если
В высказываниях нас не интересует содержательная часть, а только значения истинности (0 или 1). Множество таких наборов конечно и равно 2 n, и функцию 
можно задать таблично. Такая таблица называется таблицей истинности формулы.
П р и м е р 1.Составить таблицу истинности формулы f = 
Для построения таблицы истинности f вычислим ее значения на каждом из восьми наборов переменных.
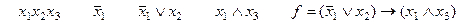
0 0 0 1 1 0 0
0 0 1 1 1 0 0
0 1 0 1 1 0 0
0 1 1 1 1 0 0
1 0 0 0 0 0 1
1 0 1 0 0 1 1
1 1 0 0 1 0 0
1 1 1 0 1 1 1
П р и м е р 2. Доказать равносильность формул
0 0 0 1 1 1 1
0 1 1 0 0 1 0
1 0 1 0 0 1 0
Левая и правая части рассматриваемой формулы принимают одни и те же значения для одинаковых наборах переменных x1 и x2, что и доказывает равносильность формул.
Как видно из предыдущих примеров, одна и та же логическая формула может быть представлена с помощью различных наборов логических операций. Существуют наборы логических операций, с помощью которых можно выразить любую логическую формулу. Такие наборы называют функционально полными системами или базисами.
Примерами функционально полных систем являются { 
}, { 
} и др. Особое значение имеет базис .
Определение. Формулы алгебры высказываний, при образовании которых не использовались операции, отличные от , называют булевыми формулами алгебры высказываний.
Дата добавления: 2015-07-20; просмотров: 88 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формулы алгебры высказываний. | | | Совершенная дизъюнктивная нормальная форма. |