Т.е. импликация ложна тогда и только тогда, когда a – истина, а b – ложь.

a – посылка, b − заключение.

Восприятию определения импликации сопротивляется, хотя в математике оно очень часто нами используется. Из арифметики известна теорема «если целое число делится на шесть, то оно делится на два» − высказывание Q. Высказывание а(x) – «число делится на шесть»; высказывание b(x) – «число делится на два», тогда Q(x) ≡ a(x) → b(x). Ясно, что при x = 6, 2, 3 реализуются четвертая, вторая и первая строки. Однако, нельзя подобрать число для третьей строки.

Но можно привести и другие примеры. Например, « если сын сдаст сессию на отлично, то отец купит ему машину. В нашем случае события а и b могут быть концептуально совсем не связаны. Возможны импликации вида «Если сегодня четверг, то 2 х 2 = 5». Эта импликация верна во все дни, кроме четверга.

Приведенные операции не являются независимыми. Одни из них могут быть выражены через другие.

Теорема 1.Справедливы следующие равносильности:

Докажем с помощью таблицы истинности первое соотношение.

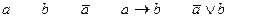
0 0 1 1 1

0 1 1 1 1

1 0 0 0 0

1 1 0 1 1

Справедливость первого соотношения доказывается тождественностью последних столбцов.

Из приведенных равносильностей видно, что → и ~ выражаются через

Можно показать, что через операции можно выразить любую операцию алгебры высказываний. Поэтому в дальнейшем основное внимание уделяется этим операциям, которые называются булевскими (булевыми) операциями алгебры высказываний. Джордж Буль (1815 – 1864) – английский математик, основатель символической логики, которую теперь принято называть булевой алгеброй.

Теорема 2. Справедливы следующие равносильности для булевой алгебры высказываний:

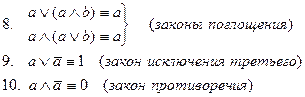
Дата добавления: 2015-07-20