|
Читайте также: |
С алгебры высказываний начинается изучение логики. Логика, созданная,как наука, Аристотелем (384-322 до н. э.), на протяжении столетий использовалась как фундамент для многих наук, включая теологию, философию, математику. Она – тот фундамент, на котором построено все здание математики. Логика – это наука, которая позволяет определить истинность или ложность того или иного математического рассуждения, исходя из некоторых первичных утверждений, называемых аксиомами. Логика применяется также в информатике при построении компьютерных программ и доказательства их корректности. Понятия и средства логики лежат и в основе современных информационных технологий.
Основными объектами традиционных разделов логики являются высказывания.
Высказывание – это утверждение или повествовательное предложение, о котором можно сказать истинно оно или ложно. Все научные истины, события повседневной жизни, ситуации, возникающие в экономике и процессах управления и т.п. формулируются в виде высказываний. Повелительные, вопросительные и бессмысленные предложения не являются высказываниями.
Примеры высказываний: « Дважды два – четыре», «Рубль – российская валюта», Сережа – брат Олега», «2 > 3», «Волга впадает в Средиземное море». Первое и второе высказывания являются истинными, четвертое и пятое ложными, третье предложение может считаться высказыванием только в определенных условиях только, когда мы знаем Сережу и Олега и, следовательно, можем сказать истинно это высказывание или ложно.
Примеры предложений, не являющихся высказываниями: Кто Вы? (вопрос), Выполните это задание к следующему занятию.
В дальнейшем нас будет интересовать не содержание высказывания, а значение его истинности («истина» или «ложь»). Таким образом, мы имеем только два класса высказываний: класс истинных высказываний и класс ложных высказываний.
Введем обозначения: если а – высказывание, то через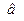 
будем обозначать значение его истинности. 
Если a – истинное высказывание, то 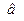=1.
Если а – ложное высказывание, то 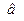= 0.
Дата добавления: 2015-07-20; просмотров: 134 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные свойства операций над множествами. | | | Отрицание. |