Алгебраические критерии устойчивости(Рауса, Гурвица и т.д)

Def: К.У. – называются признаки по которым можно судить об устойчивости САУ без решения диф. ур-ий динамики системы и без нахождения корней. Все критерии делятся на 2 группы: а) Алгебраические, которые основаны на анализе коэф. харак-го ур-я.; б) частотная, которая основана на анализе частот. характ-к системы. Простейший алгебраический критерии Стодолы. Простейшим необходимым, но недостаточным крит. уст. яв-ся требование, чтобы все коэфф. характ-го ур-я имели одинаковый знак. Док-во: Пусть мы имеем устойчивую систему с хар. ур-ем a_npⁿ+ a_n-1p^n-1+…+ a₁p+ a₀=0 (1), для устойчивости системы все корни имеют отриц. Вещественную часть. p₁=-α₁, p₁=-α₂, p_3,4=α₃±jβ₃,…, p_n=-α_n, где α и β – неотр. числа, тогда ур-е (1) можно записать a_n(p-p₁)*(p-p₂)*(p-p₃)…(p-p_n)=0, подставив значение корней a_n(p+α₁)*(p+α₂)*(p+α₃-jβ₃) * (p+α₃+jβ₃)…(p+α_n)=0. a_n(p+α₁)*(p+α₂)*[(p+α₃)²jβ₃²] …(p+α_n)=0. Раскроем скобки и приведем к исходному виду(1). Перемножая и складывая положит. числа нельзя получить отрицательные т.е все коэфф. будут положительными ур-я (1) или отрицат. в зависимости от знака а_n. Для систем I и II порядков этот критерий явл-я необходимым и достаточным. Для систем более высоких порядков(III и выше) этот критерий яв-ся необходимым т.е если хотя бы один коэф. характ-го ур-я имеет знак отличный от знака других коэф-ов, то можно сразу сказать что система не устойчива и никаких других исследов. проводить не нужно. Недостаточность критерия состоит в том что для некоторых неустойчивых систем мы можем получить все коэфф. одного знака и требуется дополнит. исследования. Были разработаны другие алгеб. критерии устойчивости которые яв-ся как необходимыми так и достаточными. Наиб. распростран. получили критерий Рауса и критерий Гурвица. Оба эти критерия в конце концов приводят к одной и той же системе неравенств. Критерий Рауса: правило постр. определителя Рауса a₀pⁿ+ a₁p^n-1+…+ a_n-1p+ a_n=0. 1-я строка: заполняется коэфф. с четными индексами, 2-я строка: заполняется коэфф. с нечетными индексами,

3-я строка и последующая получ. вычислением из предыдущих двух строк. Каждый элемент получ. перекрестным умножением элементов двух предыдущих строк

и делением элемента предыдущей строки: c_i,k=(c_i-2,k+1*c_i-1,1- c_i-2,1*c_i-1,k+1)/ c_i-1,1. Всего строк в таблице будет n+1. Постепенно справа появ-я нули и число значущих элементов умножается. Для устойчивости САУ необходимо и достаточно чтобы коэфф. 1-ого столбца таблицы Рауса были отличны от нуля и положительны (c_i,1≠0; c_i,1>0). Если хотя бы появ-ся 0 то система находится на границе устойчивости, если отриц. число то система неустойчива. Критерий Гурвица: Правило состав. опред. Гурвица. Главная диагональ определ. послед. заполняется коэфф. харак. ур-я начиная с коэфф. при (n-1) производной т.е p^n-1 и до свободного члена. Столбцы вверх от диагонали заполняют последоват. коэфф. по убыв. степ; вниз по возраст. степеням “p”. На месте коэфф. индексы котор. (>n и <0) ставят 0. a₀pⁿ+ a₁p^n-1+…+ a_n-1p+ a_n=0.

Def: Для того чтобы хар-ое ур-е системы имело все корни с отриц. веществ. частью необходимо и достаточно, чтобы главный определ. Гурвица (∆n) и все его

диагональные миноры (∆_n-1, ∆_n-2, ∆₁) имели один знак с коэфф. при старшей производной (а_n>0).

Пример: а) система I-порядка D(p)=a₁p+ a₀=0, ∆_n= |a₀|=a₀. {^a1>0_a0>0; б) система II-порядка D(p)= a₂p²+ a₁p+a₀ =0, ∆₂= |^{a1 0}_{a2 0} |, ∆₁=|a₁|=a₁; {^a2>0a1>0_a0>0; в) система III-порядка D(p)= a₃p³+a₂p²+ a₁p+a₀ =0, ∆₂= |^{a2 a0 0} a3 a1 0 _{0 a2 a0} |= a₀*∆₂=a₀* |^{a2 0}_{a3 a1} |, ∆₂=

|^{a2 0}_{a3 a1} |=a₂ *a₁ – a₀ *a₃. ∆₁=|a₂|=a₂.

W_зу(р)=((К_nK₀)/p(T₀₂²p²+T₀₁p+1))/(1+((К_nK₀)/p (T₀₂²p²+T₀₁p+1)))= (К_nK₀)/(T₀₂²p³+T₀₁p²+p+ К_nK₀ + 1), где а₃=T₀₂²p³, а₂=T₀₁p³, а₁=p, а₀=К_nK₀.

а₁а₂>а₃а₀, T₀₁>T₀₂²*К_nK₀,

К_n ≤ T₀₁/ T₀₂²*К_nK₀. При равенстве система будет находиться на границе устойчивости. Значение варьированного параметра при которой

система наход. на границе устойчивости назыв. критическими. Недостаток алгебр. критерия: они дают ответ устойчива система или нет и ничто не говорят что надо сделать чтобы система стала устойчивой. С инженерной точки зрения более удобным оказываются частотные критерии.

18. Частотные критерии устойчивости:(Михайлова, Найквиста и т.д)

Принцип аргумента: Пусть задано хар-е ур-е D(p)=a_npⁿ+ a_n-1p^n-1+…+ a₁p+ a₀=0, Это уравнение можно записать через его корни D(p)= a_n(p-λ₁) * (p- λ ₂)*(p- λ ₃)…(p- λ _n)=0, λ ₁, λ ₂, λ ₃, λ _n – корни полинома D(p). Сделаем подстановку p=jω и перейдем в частотную область D(jω)= a_n(jω -λ₁ ) * (jω - λ ₂)*(jω - λ ₃)…(jω - λ _n)=0. Представим элементарный множитель (jω-λ _i) в виде вектора на комплексной плоскости и рассмотрим его поведение при изменении частоты ω от -∞ до +∞.

Для корня с отриц. вещественной частью вектор jω-λ_i будет поворачиваться против часовой стрелки в положит. направлении на 180⁰. Обозначим этот разворот как приращение аргумента

элементарного вектора: ∆arg(jω-λ_i)=+π, ω(-∞;+∞). Для корня с положит. веществ. частью это приращение составит: ∆arg(jω-λ_i)=-π. Если система устойчива, то все n-корней лежат слева мнимой оси и приращение аргумента функции D(jω). ∆arg[D(jω)]=+π*n, (-∞;+∞). Если рассматривать только положит. значение частоты т.е ω(0,+∞) то приращение составит: ∆arg[D(jω)]=(π/2)*n. Критерий уст-ти Михайлова: Используя принцип аргумента исследуем поведение ф-ии D(jω) при изменении частоты ω(0;+∞). D(jω)=a_n(jω)ⁿ+ a_n-1(jω)^n-1+…+ a₁(jω)+ a₀=R(ω)+jQ(ω). Для каждого значения частоты ω имеем вектор, который будет поворач. при изменении частоты. Траектория конца вектора назыв. траекторией годографа Михайлова. В соотв. с принципом аргумента можно сфор. кр. Михайлова: Def САУ будет устойчива если годограф функции D(jω) начинается на положительной вещественной полуоси и проходит послед. n-квадрантов нигде не нарушая порядок следоват. квадрантов и не обращаясь в 0.

Условие нахождения системы на границе устойчивости: D(jω)=0,при {^R(∞)=0_Q(∞)=0 D(p)= T₀₂²p³+T₀₁p²+p+ К_nK₀, D(jω)=

T₀₂²(jω)³ +T₀₁(jω)²+(jω)+ К_nK₀=(К_nK₀-T₀₁ω²)- jω (T₀₂²ω² -1). {^{КnK0-T01ω2=0} _{T022ω2 –1}, ω²= К_nK₀/T₀₁, (T₀₂² *К_nK₀)/ T₀₁=> K_nкрит= T₀₁/T₀₂²K₀. Формулировка критерия Мих-ва может быть изменена:

Для устойчивой САУ годограф начин. на положит. веществ. полуоси и должен поочередно пересекать

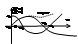мнимую и веществ. оси. Построим R(ω), Q(ω).

Вывод; для уст-й. САУ ф-ии R(ω) и Q(ω) должны по очереди пересек. ось абцисс, корни R и Q должны

чередоваться. Крит. уст-ви Найквиста: В отличии от ранее рассмот. крит. уст-ви. кот. опирались на соотв. исслед. системы хар-ки. Крит. Найквиста осн-н на анализе АФХ, КЧХ разом. системы по виду кот. судят об уст-ти замкн. системы. Причем АФХ может быть использ. как аналит. так и эксперим. Пусть имеем след. систему: W_з(p)=W_p(p)/1+W_p(p)

для систем 1-ой обрат. связью, W_p(p)=W₁(p)*W₁(p),W_p(p)=

М(р)/D(p) при (m≤n).Учитывая это получим W_з(p)= М(р)/(D(p)

+М(р))=М(р)/D_з(p).Устойчив.

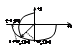замкнутой системы определ. хар-им ур-ем: D_з(p)=D(p)+М(p)=0. Ур-е анолог. годогр. Михайлова для замк-ой системы имеет вид: 1+ W_p(p)=0, 1+ W_p(jω)=0, W_p(jω)=-1. т.е крит. точка смещ. в т. с коорд.(-1; j0). Рассмот. повед. век-ра

1+W_p(jω)=F(jω)-вектор F(jω)=1+М(jω)/(D(jω)= D_з(jω)/D(jω). Применим принцип аргумента: ∆argF(jω)= ∆arg

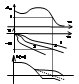
D_з(jω)- ∆argD(jω). Чтобы замкн. система была устойч. необход. чтобы все корни D_з(jω) имели отриц. веществ. часть, но если корни слева, то тогда: ∆argD_з(jω)=(П/2)*n. Пусть разомк. система не устойч. и имеет r-корней с положит. веществ. частью тогда: ∆argD(jω)=((n-r)*П/2)-r*П/2. и общее приращ. ф-и будет: ∆argF(jω)=((П/2)*n)-((n-r)*П/2)+r*П/2=(П/2)*2r. Получ. результат треб. для устойч. замк. САУ чтобы вектор F(jω) совершил r/2 оборотов в положит. направл. Def: замкн. САУ будет устой-ва если АФХ разом. сист. охватыв. точку с коорд.(-1; j0) r/2 раз, где r- число корней хар-ого ур-я раз. сист. с положит. веществ. частью. Если раз. сист. устой-ва т.е r=0, то фор-ка упрощ. Def: замк. САУ будет уст. Если АФХ раз. сист. неохват. т.(-1; j0).

Замк. САУ будет уст-м если АЧХ разом. сист. станет <1. раньше чем ФЧХ достигнет знач.

-П,φ(ω)=-П. Для ЛАЧХ: замкн. САУ будет уст. если ЛАЧХ

раз-ой сист. станет <0дБ, раньше чем ФЧХ достигнет знач. –П.

Дата добавления: 2015-07-25