Типовые динамические звенья (временные и частотные характеристики, передаточные функции).

у

х

При исследов. сложных технич. систем широко применяется принцип декомпозиции тюе разбиение сложного на простые составляющие. Теория управ-я использует разбиение сложных САУ на элементарные звенья назыв. типовыми динамическими звеньями. Типовыми назыв. звенья динамика которых описыв. диф. ур-ми не выше второго порядка. Для описания большинсва реально технических систем достаточно типовых динам. звеньев: 1) Безинерц. усилит. звено: m=0, n=0 (b₁=0, a₂= a₃=0). a₀Y(t)=b₀X(t). Выходной сигнал пов-яет без искажения по ф-ме и без сдвига по времени входной сигнал

у(t)=(b₀/a₀)*x(t), b₀/a₀=k[^{ед.изм.вых}/_{ед.изм.вх.}];

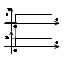x(t)=1(t), h(t)=k*1(t)

OФ: Y(p)=kX(p);

ПФ: W(p)=Y(p)/X(p)=k;

АФХ: W(jω)=k;

ВЧХ: P(ω)=k;

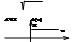МЧХ: Q(ω)=0;

АЧХ: A(ω)= P²+Q² =P

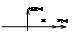ФЧХ: φ(ω)=arctgQ/P=artcg0=0.

АФХ

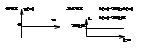
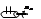2) Инетгрирующее звено: m=0,n=1,a₀=0. a₁p*Y= b₀x. a₁*(dy/dt)=b₀x/a₁, b₀/a₁=Kи [1/c]-коэф. добротности. 1/Ки=Ти [c], ∫dy=∫К_иxdt, y(t)=Ки∫xdt.

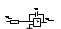Ω=dα/dt, α=∫Ωdt. W(p)= Zoc/Zвх, Zвх=R, Zвх=1/Cp, Rc=Tи. W(p)=1/Rcp=1/Тиp= Ки/р. П.Х. x(t)=1(t),

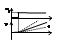y(t)=Ки∫1dt = Ки*t=t/Ти.Ки- коэф. добротности влияет на наклон переход. характеристики. Ти- равно времени за которое входная величина

меняется на1. dy/dt=Ки*х. p*Y= Ки*х. ПФ. W(p)

=Y(p)/X(p)=Ки/p=1/Тир- перед. ф-я

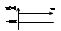
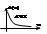
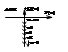интегрирующего звена. АФХ W(jω)=1/jTω=-j* 1/Tω. Видно что АФХ расположена на отриц. мнимой оси.

ВЧХ: P(ω)=0; МЧХ: Q(ω)=-1/Tω; АЧХ: A(ω)= P²+Q² =|Q|, A(ω)=1/Tk*ω=Ки/ω; ФЧХ: φ=arctgQ/P =arctg(-∞)=-П/2. A(ω)=Ки/ω, L(ω)=20lgA(ω)= 20lgКи - 20lgω. L(1)=20lgКи. 3) Дифф-ое звено

описывается уравнением: a₁*(dY/dt)+ a₀Y = b₁*(dY/dt) или a₁*PY+a₀*Y=b₁*PX, в канонической форме: (TP+1)Y=KPX где T=a₁/a₀, K=b₁/b₀, передат-я ф-я звена Y/X=Wрд(p)=K*P/T*P+1. Реальные дифференцирующие звенья имеют такую передаточную функцию. Очевидно, что чем меньше Т, тем ближе реальное звено по свойствам приближается к идеальному.

4) Апериодич. звено I-го порядка

a₁*(dY/dt)+ a₀Y = b₀Х. Это уравнение является линейным дифференциальным уравнением первого порядка. Для того, чтобы определять свойства звена по величине его параметров, уравнение представляется в канонической форме

T*(dY/dt)+Y=K*X или TPY+Y=K*X, где T= a₁/a₀ [c]-пост. врем. Звена, K=b₀/a₀-коэф. передачи звена. В частности, при T ® 0 получаем безинерционное звено. Получаем: Y/X= Wа(p)=K/TP+1 5) Интегрир. звено II-го порядка: а) апериод. звено II-го порядка, б) колебат. звено II-го порядка:

описыв. ур-ем a₂*(dY²/dt²)+ a₁*(dY/dt)+ a₀Y = b₀*Х но не выполн. условие а₂р²+ а₁р+ а₀=0, тогда в канонической форме T²P²Y²+ 2ρ*TPY=КХ, где Т

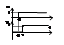
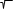
= a₂/a₀ – пост. времени, ρ=а₁/2* а₂ – показ. колебательности,

 

Для колебательного звена0< r < I. При r > I получается апериодическое звено второго порядка. При r = 0 получаем два чисто мнимых корня, что соответствует передаточной функции так называемого консервативного звена W(p)=K/T²P²+1 в) консерват. колебат. звено. 6) Звено чистого запаздывания: выходной сигнал звена повтор. вход. без искажения по форме, но с искажением вовремени.

τ=ℓ/υ, y(t)=χ(t-τ),

h(t)=1(t-τ). В

операт. виде:

y(t)=х(t-τ), Y(p)=

X(p)e^-τp. ПФ: W(p) =

Y(p)/X(p)=e^-τp; АФХ: W(iω)=e^-τiω=cosωτ – jsinωτ; ВЧХ: P(ω)=cosωτ; МЧХ:Q(ω)=-sinωτ; АЧХ: A(ω)=

АЧХ

P²+Q² = cos²ωτ+sin²ωτ =1; ФЧХ: φ(ω)=arctgQ/P = arctg –sinωτ/cosωτ = -arctg tgωτ=-ωτ; ЛАЧХ: L(ω)=20lg(ω)=0.

Дата добавления: 2015-07-25