Связь устойчивости с корнями характеристического уравнения САУ. Теоремы Ляпунова.

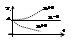Пусть динамика линейной САУ описыв. ур-ем: [a_npⁿ+ a_n-1p^n-1+…+ a₁p+ a₀]*Y(p)= [b_mp^m+b_m-1p^m-1 +…+ b₁p+ a₀]*X(p). Применим к системе внешнее воздействие Х(р) т.е выведем ее из равновесия, а затем снимем внешнее воздействие. Это соотв-ет правой части равное 0. [a_npⁿ+ a_n-1p^n-1+…+ a₁p+ a₀]*Y(p)=0. Это ур-е будет описывать собств. движение системы. В общем случае выходная вел-на Y(p)≠0, тогда a_npⁿ+ a_n-1p^n-1+…+ a₁p+ a₀=0 – это ур-е характеристическое ур-е. Через корни харак-го ур-я можно представить решения исходного диф. ур-я. Каждому корню будет соотв. составляющая. Рассмотрим влияние корней на переходные процессы в системе: 1) веществ. корень p_i. В решении будет составл. веществ. A_ie^pit. а) p_i>0 =>e_t→∞ ^pit→∞ расход. процесс, система не устойчива; б) p_i<0 =>e_t→∞ ^pit→0 сход. перех. процесс, система устойчива; в) p_i=0 =>Аe^pit=А_i – перех. процесса нет.

2) пара комплексно сопряженных корней p_1,2=α_i±jβ_i. Ему в решении будет соотв-ть составл.

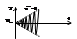вида: c₁e^p1t+c₁e^p2t= A_ie^αit*sin(β_it+φ_i),где e^(α+jβ)t, e^(α-jβ)t, c₁,c₂, A_i, φ_i-постоянная интегрирования. а) α_i>0, тогда e_t→∞ ^αit→∞. Имеем расход. переходный процесс, система будет неустойчива:

б) α_i<0, тогда e_t→∞ ^αit→0. Этому соотв. график:

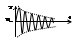
в) α_i=0, p_1,2=±jβ_i, A_isin(β_it+φ_i), этому соотв. график:

г) α_i=0, β_i=0, c₁+c₁= A_i*sinφ_i=const. Имеем нейтрально устойчивую систему т.е

переходного процесса нет:

Вывод: для устойчивости САУ необходимо и достаточно чтобы все корни харак-го ур-я имели отрицат. вещественную

часть т.е они распол. в левой плоскости. Реальные системы не линейны и мы их линеаризуем. Теоремы Ляпунова: 1) Если линеариз. система автомат. управл-я устойчива, то не какие из отображенных при линеаризации корней не могут сделать ее неустойчивой. 2) Если линеар. САУ неустойчива, то никакие из отброшенных корней при линеариз. не могут сделать ее устойчивой 3) Если линеариз. САУ находиться на границе устойчивости, то отброшен. при линеаризации корни могут сделать ее как устойчивой так и нет.

Дата добавления: 2015-07-25