|
Читайте также: |
Дискретная система автоматического регулирования устойчива, если переходные процессы в ней затухает с течением времени.
По аналогии с непрерывными, выражение для реакции ДАС на произвольный входной сигнал g(t) может быть представлена в виде суммы переходной xп и установившихся xу составляющих
x[n,e]= xп[n,e]xу[n,e]
С математической точки зрения определение устойчивости сводится к выполнению равенства
|
Ранее полученное выражение для переходной составляющей имеет вид:
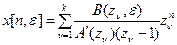
Из этого выражения следует очевидное условие устойчивости
.
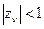Иными словами, для устойчивости необходимо, чтобы все корни характеристического полинома A(z) замкнутой системы (полюсы передаточной функции замкнутой системы)
A(z)=a0zk+a1zk-1+..+ak
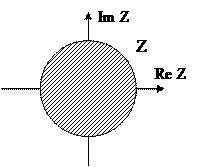были расположены внутри окружности единичного радиуса в плоскости комплексного переменного z.
Таким образом, исследование
устойчивости ДАС сводится к
изучению расположения корней
относительно единичной
окружности.
При этом следует иметь в виду что ДАС реагирует не на сигнал g(t), а на g[n] из-за наличия импульсного элемента.
Поэтому условие 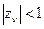гарантирует затухание переходной составляющей только в дискретные моменты nT, т.е. возможны случаи (крайне редкие) “скрытой” неустойчивости, когда xп[n] затухает, а x(t) не затухает или расходится.
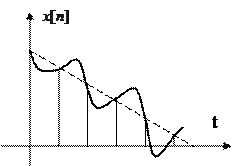При исследовании устойчивости
ДАС могут применяться все
критерии устойчивости
непрерывных систем.
Дата добавления: 2015-07-20; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Учитывая, что Ф(z,e) является дробно-рациональной по отношению к переменной z и обозначая | | | Критерий Рауса-Гурвица. |