Определение процессов в импульсных системах при типовых воздействиях.

При исследовании импульсных САР обычно интересуются процессами, возникающими на выходе системы при некоторых типовых воздействиях, приложенных ко входу. Ими являются, например еденичное ступенчатое или гармоническое воздействие.

Применим Z -преобразование для определения реакции импульсной системы на указанные воздействия при нулевых начальных условиях.

Пусть передаточная функция замкнутой системы Ф(z,e).

Изображение g(t)=1[t].

G[z] =Z{1[t]}=z/(z-1)

В этом случае процесс на выходе системы можно определить по формуле

x [n,e]=Z^-1{Ф(z, e)·G(z)} или

x [n,e]=Z^-1{Ф(z, e)·z/(z-1))}

Для вычисления обратного Z-преобразования воспользуемся формулой (теорема вычетов)

	x [n,e]= Res Ф(z,e) ·z/(z-1) n·z^n-1½z=z

где вычеты берутся в полюсе z₀=1 и в полюсах 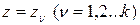передаточной функции Ф(z, e). Будем предполагать (для простоты изложения) что все полюсы ненулевые.

Найдем вычет в точке z₀=1 по формуле

.

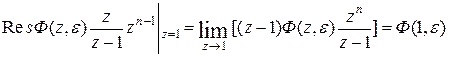Дата добавления: 2015-07-20