Для решетчатых функций вводится понятие конечных разностей и сумм, которые в некотором смысле соответствуют понятиям производной и интеграла для обычных функций.

Выражение Df[n] = f[n+1] – f[n] (1)

называется конечной разностью первого порядка решетчатой функции. Для краткости Df[n] называют просто первой разностью. Первая разность от решетчатой функции Df[n] называется разностью второго порядка решетчатой функции f[n] или просто второй разностью, т.е.

D²f[n] = Df[n+1] - Df[n] (2)

Разность k-го порядка решетчатой функции f[n]

D^kf[n] = D^k-1f[n+1] - D^k-1f[n] (3)

Разность любого порядка можно выразить через значение решетчатой функции f[n]. В частности для второй разности получим

D²f[n]= Df[n+1]-Df[n]={f[n+2]-f[n+1]}-{f[n+1]-f[n]}= f[n+2]-2f[n+1]+f[n] (4)

Аналогично для третьей разности найдем

D³f[n]= f[n+3]-3f[n+2]+3f[n+1]-f[n] (5)

Для разности k-го порядка справедлива формула

D^kf[n] = (-1)ⁿ()f[n+k-n], (6)

где ()= C_kⁿ=

Полученные формулы, определяющие разности решетчатых функций, позволяют выразить саму решетчатую функцию f[n] через разности различных порядков. Так из (1) получим

f[n+1]= f[n]+ Df[n] (7)

Из (1) и (2)

D²f[n]=f[n+2]-f[n+1]-Df[n]=f[n+2]-f[n+1]+f[n+1]-f[n]-2Df[n]=f[n+2]-f[n]-2Df[n]

Откуда f[n+2]=f[n]+2Df[n]+ D²f[n]

Продолжая, получим следующую формулу

f[n+l]= ()D^k f[n] (8)

или в частности при n=0

f[l]= ()D^k f[0] (9)

Формулы (8) и (9) выражают значение решетчатой функции через ее конечные разности до порядка l включительно. Эти формулы являются дискретным аналогом разложения непрерывных функций в ряд Тейлора.

Пример. f[n] = a, где a- cont. Найти D f[n]

D f[n]=f[n+1]-f[n]= a-a=0

f[n]=an+b, найти D f[n]

D f[n]=a(n+1)+b-an-b=a

D² f[n]= D a=0

f[n]=n²

D f[n]=(n+1)²-n²=2n+1

D² f[n]= D f[n+1]- D f[n]=2(n+1)+1-2n-1=2

D³ f[n]=0

f[n]=e^{a n}

D f[n]= e^{a (n+1)}- e^{a n}= e^{a n}(e^a -1)

D² f[n]= (e^a -1) D e^{a n}= e^{a n}(e^a -1)²

D^k f[n]= e^{a n}(e^a -1)^k

Рассмотрим теперь операцию, которая является обратной по отношению к операции взятия конечной разности. Пусть решетчатая функция f[n] определена при положительных значениях аргумента n=0, 1, 2,… Требуется найти такую решетчатую функцию F[n], для которой функция f[n] является первой разностью.

Эта задача аналогична задаче о нахождении первообразной в анализе обычных функций. Искомая функция имеет вид

F[n] = 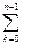f[k] (n=1,2,…)

Действительно,

DF[n]= F[n+1]-F[n]= f[k]- 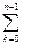f[k]= f[n]

Функцию F[n] называют первообразной для f[n].

Если решетчатая функция f[n] определена при всех целочисленных значениях аргумента n=0,±1, ±2, … то для определения первообразной необходимо дополнительно потребовать, чтобы при каждом конечном n сходился ряд f[k]. При этом условии первообразная определяется выражением

F[n]= f[k].

Если функция F[n] является первообразной для f[n], то и функция F[n]+C, где С = const, также является первообразной для решетчатой функции f[n]. Действительно

D[F[n]+C]= DF[n]+ DC=f[n].

Таким образом, общий вид первообразной для решетчатой функции f[n] определяется формулой

F[n]= f[k]+C

Значение постоянной С можно выразить через значение первообразной при некотором фиксированном значении аргумента n=N

C=F[N] - 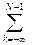f[k]

Подставляя это выражение в предыдущее, найдем

F[n]= f[k]+F[N] - 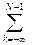f[k]= f[k]+F[N]

Откуда

F[n]-F[N]= f[k] для любого n>N

Последняя формула является аналогом соответствующей формулы интегрального исчисления, связывающей интеграл с первообразной. Ее можно записать в виде

F[N+l]-F[N]= 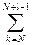f[k]= f[N+n] (l=1,2,…)

Сумму, стоящую в правой части этого выражения, иногда называют определенной суммой по аналогии с определенным интегралом.

Дата добавления: 2015-07-20