Читайте также:
|
Наряду с функциями, определенными на всей вещественной прямой t, можно рассматривать функции, которые определены только в некоторых точках t1,t2… Такие функции называют решетчатыми. Мы будем рассматривать функции, определенные только в равноотстоящих точках t=nT, где n - любое целое число, а T - постоянная, называемая периодом дискретности. Эти функции принято обозначать f[nT].
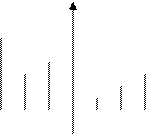f[ nT]
 |
-3Т -2Т -Т 0 Т 2Т 3Т
Любой непрерывной функции f(t) можно поставить в соответствие некоторое множество решетчатых функций, если представить переменную t в виде
t=nT+eT (0£e£1)
При каждом фиксированном значении переменной e функцию f(nT+eT) можно рассматривать как решетчатую функцию, определенную в точках eT, (e+1)T, (e+2)T,… Такие функции называются смещенными решетчатыми функциями. Для них принято обозначение f(nT+eT)=f[nT, eT]. Изменяя e в пределах от 0 до 1, можно получить множество смещенных решетчатых функций f[nT, eT], соответствующих данной непрерывной функции f(t).
f[t]
f[nT,0]
-T 0 T 2T 3T
f[nT,ε1T]
ε1T
f[nT,ε2T]
ε2T
Благодаря непрерывности функции f(t), функция f[nT, eT] является непрерывной по аргументу e и удовлетворяет условию:
f[(n-1)T, T]=f[nT, 0]
Если функция f(t) терпит разрыв непрерывности первого рода в точках t=nT, то написанное равенство не выполняется поскольку
lim f[(n-1)T, eT] ¹ lim [nT, eT]
e®1 e®0
В этом случае под значением функции будем понимать предел справа.
f[nT] = lim f[nT, eT]
e®0
Дата добавления: 2015-07-20; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные положения. | | | Для решетчатых функций вводится понятие конечных разностей и сумм, которые в некотором смысле соответствуют понятиям производной и интеграла для обычных функций. |