Критерий Рауса-Гурвица.

Критерий Рауса-Гурвица в рассматриваемом случае можно применить, если выполнить конформноеотображение плоскости комплексного переменного z на плоскость комплексного переменного w таким образом, чтобы единичная окружность |z|=1 перешла в мнимую ось на плоскости переменного w, а внутренность единичного круга |z|<1 отобразилась на левую полуплоскость Re w<0. Такое отображение выполняется с помощью дробно-линейного преобразования.

Выполняя замену переменной в

многочлене A(z) получим

a₀ (^(1+w)/_(1-w))^k + a₁ (^(1+w)/_(1-w)^k-1 +..+ a_k = ^A1(w)/_(1-w)^k

где A1(w)- многочлен степени k новой переменной w.

Например, при k=2

A1(w)=a₀ (1-w) ²+a₁(1+w)(1-w)+a₂(1-w) ² =

=a₀+2a₀w+a₀w²+a₁ - a₁w²+a₂-2a₂w+a₂w²=

=b₀w²+b₁w+b_2,

где

b₀= a₀ -a₁ +a₂

b₁= 2a₀ -2a₂

b₂= a₀ -a₁ +a₂

Исследование расположения корней многочлена A1(W) можно проводить с помощью критерия Гурвица, имеющего совокупность определителей

D₁ =b₁, D₂ = ,

.

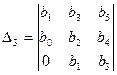Рассмотренный алгебраический метод позволяет определить является ли система асимптотическиустойчивой, однако не дает возможности исследовать устойчивость в тех случаях, когда корни A(z) лежат на самой единичной окружности |z|=1. Недостатком метода является значительная трудоемкость вычислений. Метод весьма громоздок при синтезе САР. Более удобными являются частотные методы, которые рассмотрим ниже.

Частотные характеристики

При исследовании дискретных систем широко используются частотные методы. Для получения частотной передаточной функции необходимо в выражение для передаточной функции сделать подстановку z=e^{j 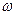T}

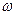W(e^{j T})= .

Частотные характеристики в этом случае (АФХ, АЧХ, ФХ) оказываются периодическими функциями частоты 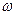с периодом .

Более удобным для получения частотных характеристик и, в частности, логарифмических является использование псевдочастоты. Обычно для этого применяют w – преобразование, при помощи которого окружность единичного радиуса e ^{j 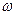T} отображается на мнимую ось комплексной величины w с помощью подстановки

или

Сделав подстановку 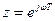, получим

где - относительная псевдочастота.

В дальнейшем изложении будем использовать, так называемую абсолютную псевдочастоту

.

При малых частотах (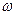 < ) абсолютная псевдочастота практически совпадает с обычной частотой , т. к. в этом случае .

Это является весьма удобным, т. к. в этом случае частотные характеристики в функции псевдочастоты практически сливаются с частотными характеристиками, построенными в функции обычной круговой частоты 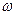. Построение же характеристик в функции псевдочастоты оказывается значительно более простым.

Нетрудно заметить, что при изменении частоты в пределах 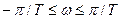, , а комплексная величина w движется по мнимой оси от до .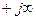

.

Аналогично для разомкнутой системы

.

Для получения частотной характеристики необходимо сделать подстановку

.

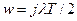Однако, как и ранее следует учитывать особый вид функции ,которая не равна W(s) при s=j 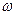и не равна W(z) при z=j .

Пример. Пусть передаточная функция разомкнутой системы имеет вид:

.

Частотная характеристика может быть получена подстановкой . Тогда

.

Построение ЛАХ и ЛФХ по этому выражению даже в этом простейшем случае вызывает затруднения. Перейдем к псевдочастоте. Тогда

.

Построение асимптотической ЛАХ и ЛФХ в этом случае не вызывает никаких затруднений.

Дата добавления: 2015-07-20