Учитывая, что Ф(z,e) является дробно-рациональной по отношению к переменной z и обозначая

Ф(z,e)= B(z,e)/ A(z),

где A(z) и B(z) – полиномы относительно z

и, представляя

,

найдем

т.к.

.

В результате получим

,где

.

Полученное выражение характеризует реакцию импульсной системы на единичное ступенчатое воздействие. Первое слагаемое, описывает установившийся процесс в системе, а второе - переходный.

Действительно, определим

Аналогично можно найти реакцию системы на гармоническое воздействие

g[n]=A₁cos( ₁n+j), получим, после окончания переходного процесса, установившийся процесс.

x_y[n,e]=A₁| Ф(j 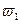,e)| ·cos[ ₁n+ j+arg Ф(j 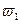,e)]

Функция Ф(j ,e) получающаяся из передаточной функции Ф(e^q,e) при q=j , называется амплитудно-фазовой частной характеристикой импульсной системы. Физический смысл тот же, что и в непрерывных системах.

В отличие от непреывных систем, частотные характеристики импульсных систем являются периодичискими функциями с периодом 2p, что следует из периодичности изображений

Ф(j ,e)=Ф[j( +2pr),e] (r=0,±1,±2...,)

Поэтому частотная характеристика Ф (j ,e) полностью определяется своими значениями в интервале шириной 2p. Обычно рассматривают интервал - p< £p. Импульсная система при 0<e£1 описывается семейством частотных характеристик. Однако при исследованиях, в ряде случаев достаточно знать частотную характеристику только при одном значении e=1.

Дата добавления: 2015-07-20