Расчет дискретных корректирующих средств.

Корректирующие средства могут быть реализованы на ЭВМ, включенной в контур регулирования. Для этого формируется требуемый алгоритм ее работы, который определяется передаточной функцией D(z). Дискретные корректирующие средства могут быть также осуществлены на дискретных фильтрах и других цифровых устройствах.

Пусть тем или иным путем найдена желаемая дискретная передаточная функция разомкнутой системы

W_ж(z)=^Фж(z)/_[1-Фж(z)]=D(z)W(z)

где Ф_ж(z) – желаемая передаточная функция замкнутой системы

W(z) – передаточная функция исходной нескорректированной системы.

Тогда искомая передаточная функция ЦВМ имеет вид

D(z)=^Фж(z)/_[1-Фж(z)] · ¹/_W(z)

Формирование желаемой функции Ф_ж(z) производится с учетом некоторых ограничений.

1. Необходимо, чтобы передаточная функция Ф_ж(z) содержала в качестве своих нулей все те нули передаточной функции W(z), модуль которых равен или больше единицы.

2. Кроме того, необходимо, чтобы выражение 1-Ф_ж(z) содержало в качестве своих нулей все те полюсы W(z), модуль которых равен или больше единицы. Невыполнение этих условий вызывает нарушение требований к грубости системы и вызывает ее неустойчивость, так как приводит к неустойчивым линейным программам ЦВМ, которые должны реализовать получающуюся по полученной формуле передаточную функцию D(z).

3. Кроме того, получающаяся дробно-рациональная передаточная функция D(z) не должна иметь степень числителя выше, чем степень знаменателя, так как это приводит к необходимости знания будущего значения входного сигнала, что не может быть реализовано.

Пример. Передаточная функция непрерывной части W₀(s)=K₂/s²; K₂=1с^-2; T=1c. Определить закон управления, реализуемый при помощи ЦВМ, который обеспечил бы системе конечное время переходного процесса.

Дискретная передаточная функция непрерывной части системы

Желаемую передаточную функцию замкнутой системы возьмем в виде

Ф_ж(z)= 0.5(z^-1+z^-2)

X(z)=Ф(z)G(z)=0.5(z^-1+z^-2) = =0.5z^-1+z^-2+z^-3+...  

_ z_ 0.5z²+0.5z z-1 z³-z²

При этом переходные процессы в системе будут заканчиваться за два периода дискретности

Дискретная передаточная функция ЦВМ равна

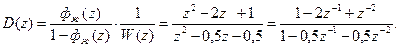
Отсюда закон уравнения, реализуемый ЦВМ, может быть записан в виде рекуррентного соотношения. Так как

D(z)=U[z]/E[z]

U[nT]=e[nT]-2e[(n-1)T]+ e[(n-2)T]+0.5u[(n-1)T]+0.5u[(n-2)T].

Дискретные корректирующие средства могут быть рассчитаны с применением дискретных частотных передаточных функций, то есть в частной области.

W_пк (jl)= W_ж(jl)/ W(jl), (*)

или соответствующие им частные характеристики

L_пк (l)= L_ж(l)- L(l).

После определения W_пк (jl) подстановкой jl=2w/T можно получить передаточную функцию W_пк(w) затем, переходя от w - преобразования к z-преобразованию подстановкой w=(z-1)/(z+1), получим W_пк(z).

Сформулированные выше ограничения по отношению к (*) имеют следующий вид:

1. Необходимо, чтобы W_ж (jl) содержала в качестве своих нулей и полюсов по переменной jl все те нули и полюсы, которые лежат в правой полуплоскости.

2. Необходимо, чтобы получающаяся дробно-рациональная функция W_пк(jl) имела степень числителя меньше, чем степень знаменателя.

Пример. Пусть в цифровой системе с экстраполятором нулевого порядка W₀(s)=K_S/s² W₀(z)=^(z-1)/_z Z{K_S/s³}=

Дискретная частотная передаточная функция

.

Примем в качестве желаемой ЛАХ L_ж ’, соответствующей типовой передаточной функции разомкнутой системы

Так как T_i<T/2; T_i=0

Дискретная частотная передаточная функция последовательного корректирующего устройства

.

Переход к передаточной функции ЦВМ дает

Выражение определяет неустойчивую программу, так как полюс передаточной функции z₁=-1 соответствует колебательной границе устойчивости. Заметим, что получившаяся W_пк(jl) не может быть реализована, вообще говоря, и в непрерывном варианте. Эта функция соответствует бесконечному подъему усиления при росте частоты до бесконечности.

Для исключения этого явления примем желаемую ЛАХ L_ж’’ в другом виде

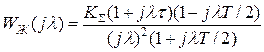
Тогда .

Переход к передаточной функции ЦВМ дает

.

Этой передаточной функции соответствует устойчивая программа ЦВМ. При этом для обеспечения запаса устойчивости, оцениваемого показателем колебательности не менее, чем М£1.5 необходимо выполнить следующие ограничения. Для базовой частоты

,

Допустимое значение малых постоянных времени

Закон управления реализуемый ЦВМ

U[nT]=b₀e[nT]+b₁e[(n-1)T], так как

То есть используется управление по отклонению и первой разности.

Дата добавления: 2015-07-20