Читайте также:
|
1. Свойство линейности. Для краткости записи приводим при e=0. Равенства справедливы и при e¹0.
Если решетчатые функции f1[n], f2[n]… fk[n] являются оригиналами и их изображения соответственно F1(z), F2(z)…Fk(z), то справедливо равенство
Z{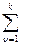 
lnfn[n]}= 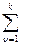lnFn(z), где ln -произвольная постоянная.
Пример. Найти изображения тригонометрических решетчатых функций sin vn и cos vn (n³0)
Z{ sin vn}=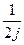 
Z{ljvn- l-jvn}= 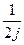[Z{ ljvn }-Z{ l-jvn }]
Используя результаты предыдущего примера, получим
Z{ sin vn }= [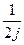 
- 
]= [ 
]= 
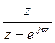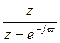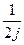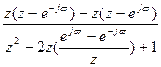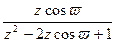
(T=1)
Аналогично для косинуса
Z{ cos vn }=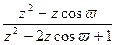 
2. Теорема смещения. Для функции времени f(t-t), где t- положительное число, причем 0£e<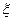 
и f(t-t)º0 при t<t<x
Z{f(t-t)= Z-(1+m)F(z, 1+e-x)},
Здесь m - целая, x- дробная часть числ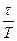а 
, а
F(z, e)= Z{f(t)} (*)
Если x£e<1, то изображение равно
Z{f(t-t)}=Z-mF(z, e-x).
В частном случае запаздывание может составлять целое число периодов дискретности т.е.
t=mT. Тогда
Z{f(t-mT)=z-mF(z, e)}
3. Теорема об умножении оригинала f(t) на экспоненту.
Если для оригинала f(t) изображение определяется формулой
F(z,e)=Z{f(t)}(*) определяемой в дискретные моменты времени t=nT+e, то
Z{elT f(t)}= deF(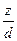
, e), где l - комплексное число, а d=elT
4. Теорема об умножении оригинала на смежную функцию.
Пусть для оригинала f(t) изображение определяется формулой (*), тогда для e=0 имеем
Z{tmf(t)}=(-1)m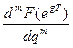 
½eqT=Z
5. Изображение конечных разностей.
Z{Dkf[n,e]}=(z-1)kF(z,e)-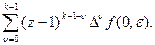 
Если дискретной последовательности f[n, e] соответствуют нули в первых k точках оси времени, т.е.
f[0, e]=f[1, e]=…f[(k-1), e)]= 0, то Dnf[0,n]=0 n=1,k-1
Тогда Z{Dkf[n,e]}=(z-1)kF(z,e).
Для обратной разности справедливо выражение
Z{Ñk f[n, e]}= (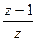
)k F(z, e),
6. Изображение конечной суммы.
Если для оригинала f(t) изображение определяется формулой (*), то
Z{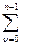 
f[n,e]}=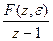 
7. Сверка решетчатых функций.
Если Z{f1[n,e]}=F1(z,e);
Z{f2[n,e]}=F2(z,e), то
Z{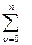 
f1[n,e]f2[(n-n)],e}= Z{ 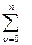f1[(n-n),e]f2[n,e]}=F1(z, e)F2(z, e)
8. Теорема о конечном значении оригинала.
Если f[n, e] - оригинал, а F(z, e)- изображение, то
lim f[n, e]=lim 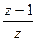F(z, e)
n®¥ z®1
9. Теорема о начальном значении оригинала. При тех же условиях f[0,e]=lim 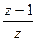F(z,e).
z®¥
Дата добавления: 2015-07-20; просмотров: 46 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Дискретное преобразование Лапласа. | | | Передаточные функции дискретных систем |